Lecture 1: Introduction to astrophysical simulations

Jan Benáček

Institute for Physics and Astronomy, University of Potsdam

October 19, 2023

1 Lecture overview

1.1 Lecture time

Table of Contents 1/2

  • 19.10. Introduction + numerical methods summary
  • 26.10. Numerical methods of differential equations — lecture + hands-on
  • 02.11. Test particle approach — lecture
  • 09.11. Test particle approach — hands-on
  • 16.11. PIC method — lecture
  • 23.11. PIC method — hands-on
  • 30.11. Fluid and MHD — lecture

Table of Contents 2/2

  • 07.12. Fluid and MHD — hands-on
  • 14.12. Radiative transfer — lecture
  • 11.01. Radiative transfer — hands-on
  • 18.01. HPC computing — lecture + hands-on
  • 25.01. Advanced — Smooth particle hydrodynamics method — lecture
  • 01.02. Advanced — Hybrid, Gyrokinetics — lecture
  • 08.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture

1.2 Computer access and skills

1.3 Evaluation

  • Mandatory presence at all hands-on sessions
  • The presence can be replaced by a homework hands-on session — individually assigned
  • Carefull! The schedule may change

2 What is plasma?

2.1 Plasma phenomenology

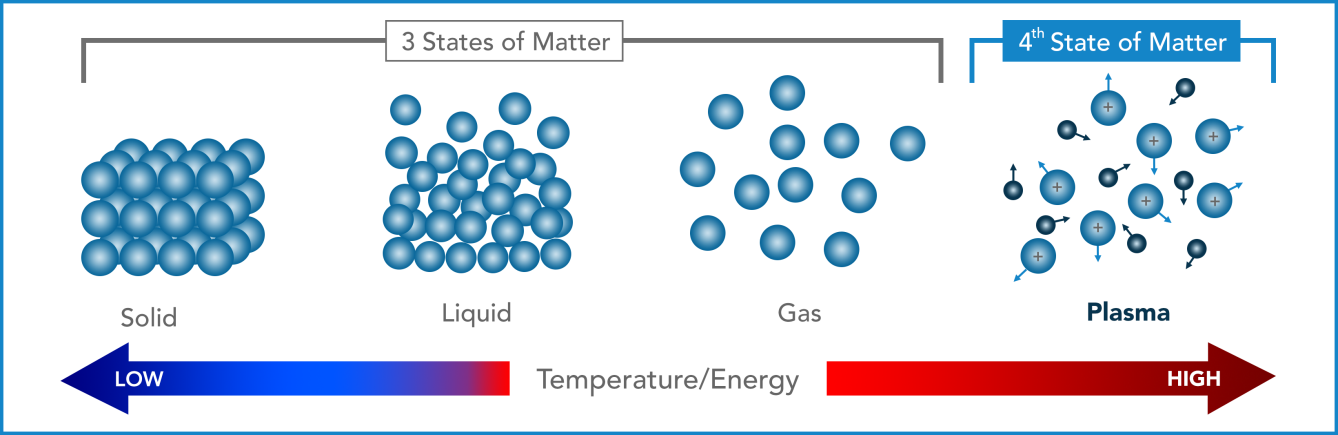
  • Partially or fully ionized (Saha equation)
  • High electrical conductivity
  • Quasi-neutral
  • Collective behaviour
  • Magnetic forces

2.2 Plasmas on Earth

Validity range of different plasma codes, credits.

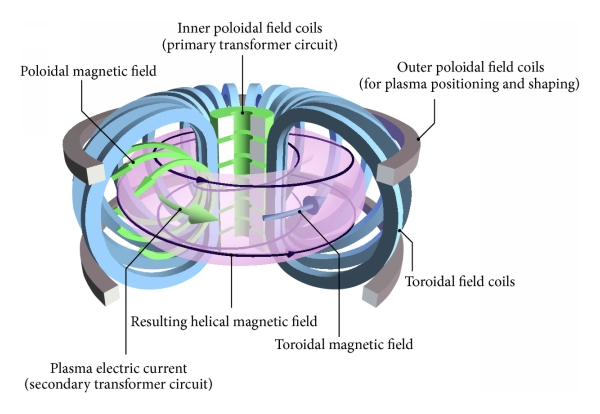
2.3 Earth’s ionosphere

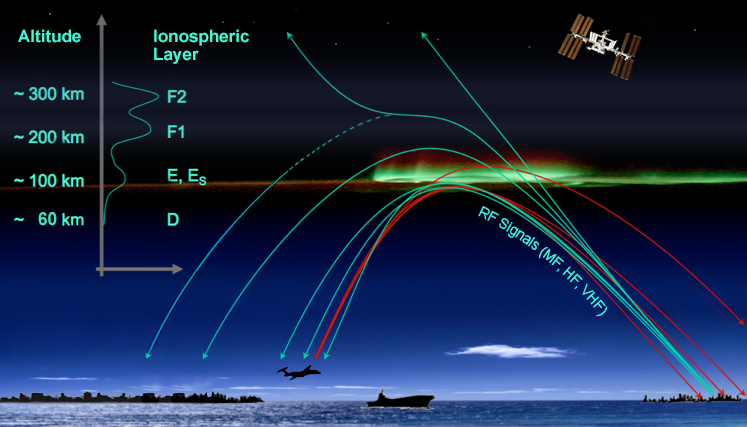
2.4 Earth’s aurora

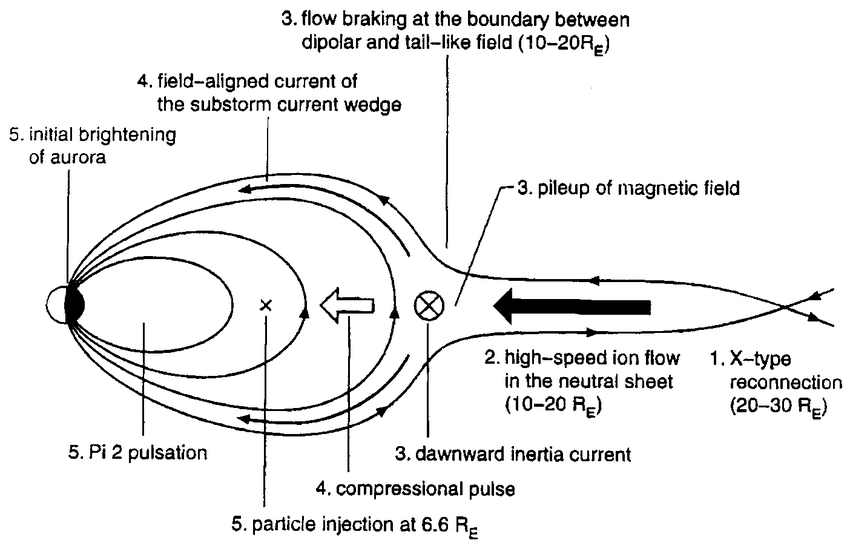
2.5 Earth’s magnetosphere

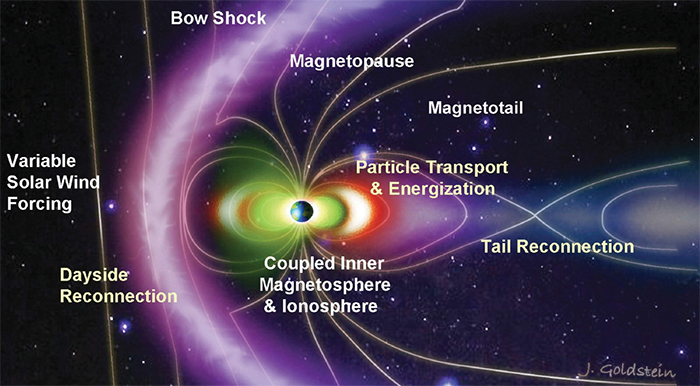
2.6 From the Sun to the Earth

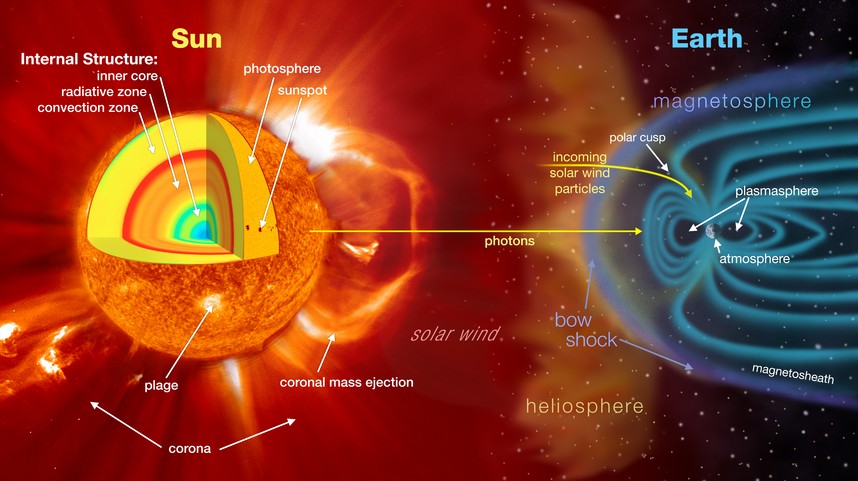
2.7 Sun/Stars

  • Solar photosphere
  • Solar atmosphere: Chromosphere, Corona.

CME eruption on the Sun (SDO)

2.8 Comets

Comet Hale Bopp 1997

2.9 Interstellar medium (ISM)

Star formation regions in the Large Magellanic Cloud

2.10 Pulsar magnetospheres

Crab Nebula

Schema of a pulsar

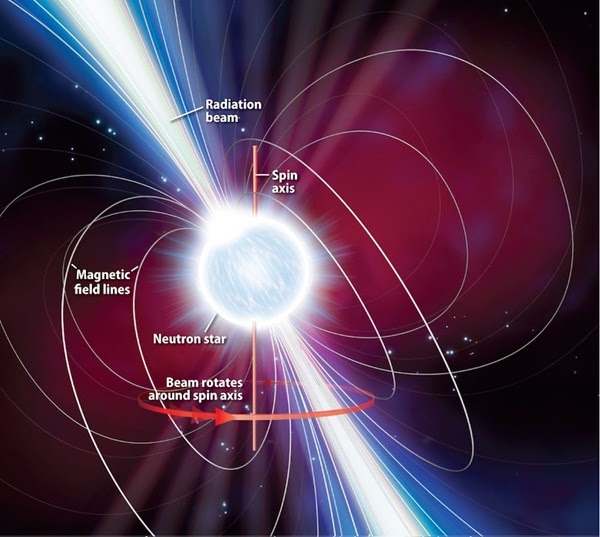
2.11 Your turn

  1. Did you have an introductory course into plasma physics?
  2. What are the main conditions to characterize the medium as a plasma?
  3. Name examples of space environments are and are not plasmas.
  4. What is your favorite space plasma environment and why?

3 Examples of astrophysical and space simulations

3.1 Examples of simulations

3.2 Your turn

  1. Did you hear about any space simulation before? Do you know more details?
  2. Did you personally run/try to run any simulation? What kind of simulation was it?
  3. How can we measure computing power that is necessary to run simulations?
  4. Can you estimate the computing power to run the simulations from previous slide?

4 Plasma properties

4.1 Plasma parameters


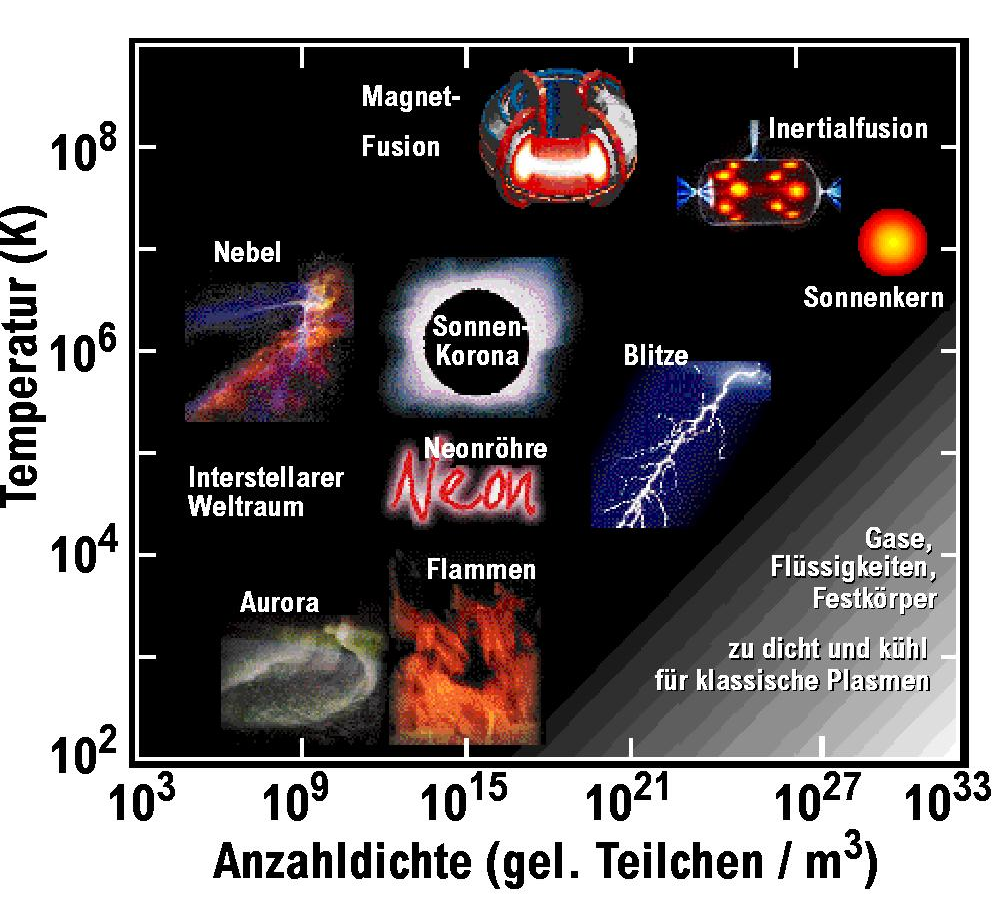
  • Temperature
  • Number density
  • Magnetic field (not in the figure)

  • Cold plasmas
  • Hot plasmas

4.2 Collisions in plasmas


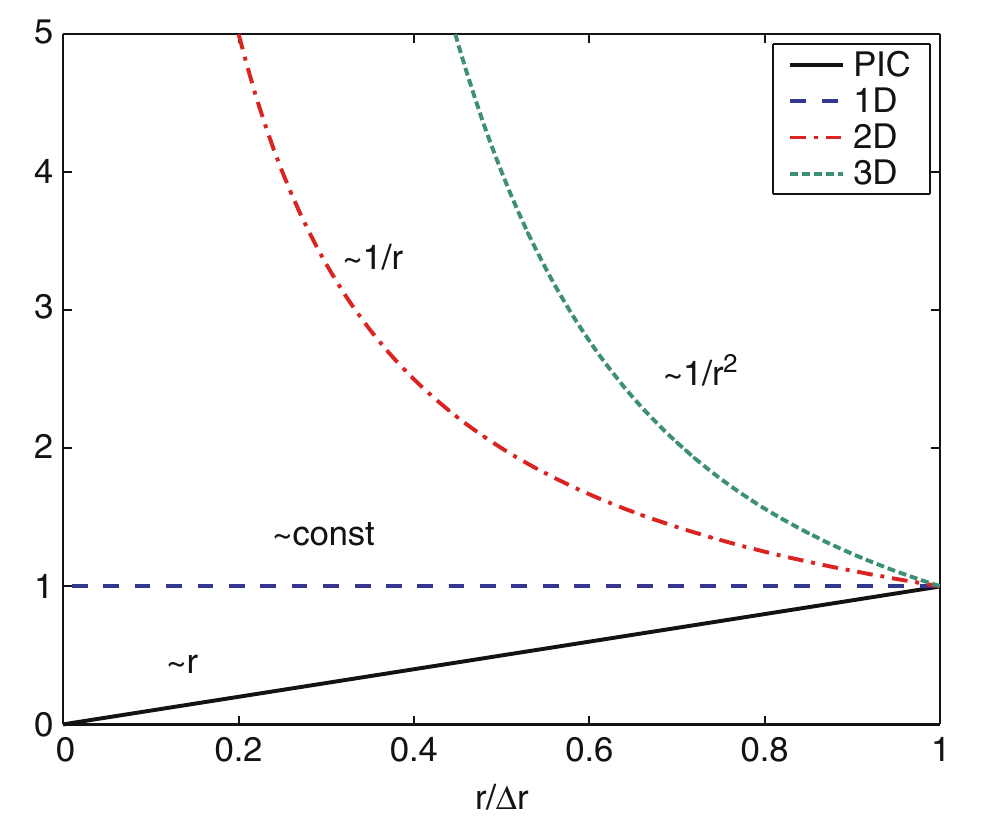
  • Plasmas can be partially or fully ionized.
  • Scattering is different: collisions among and with neutrals: large angle scattering.
  • Charged particles: smooth small angle scattering only.
  • Collisions enforce thermal equilibrium.

4.3 Length scales: Debye length

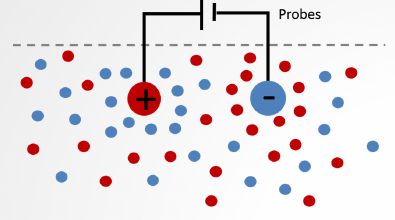
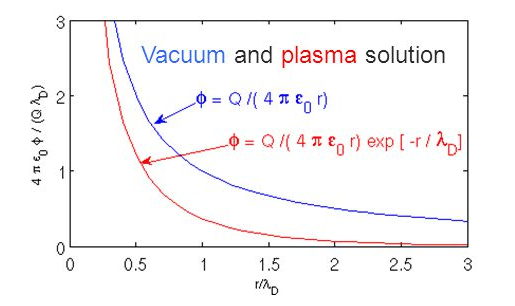
  • The Coulomb potential of each particle is shielded by other charges \[\phi_D=\frac{q}{4\pi\epsilon_0 r}\exp\left(-r/\lambda_{De}\right).\]
  • The electrostatic potential is screened out on distances larger than the Debye length \[ \lambda_{De} = \sqrt{\frac{\epsilon_0 k_B T_e}{n_e e^2}}. \]
  • The plasma is quasi-neutral only for distances \(L\gg \lambda_{De}\).
  • At sub-Debye length scales, charge separation occurs.
  • An ideal plasma must have a sufficient number of particles in a Debye sphere to enforce their collective behavior. Plasma parameter \[ N_D=n_e \left( \frac{4}{3}\pi \right)\lambda_{De}^3 \gg 1. \]

4.4 Time scales: Plasma frequency


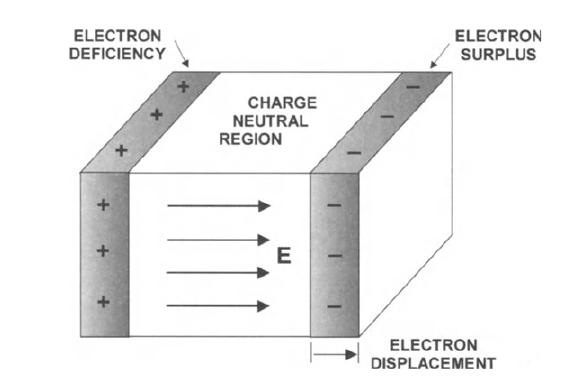
  • Plasma frequency \[ \omega_{pe}=\sqrt{\frac{n_e e^2}{\epsilon_0 m_e}}. \]
  • Typical response of electrons to restore quasineutrality when disturbed by external forces.
  • Note that \[ \omega_{pe}= \frac{v_{th,e}}{\lambda_{De}}=\frac{\sqrt{\frac{k_BT_e}{m_e}}}{\lambda_{De}}. \]
  • Collective behaviour

4.5 Time scales: Magnetic field and gyromotion

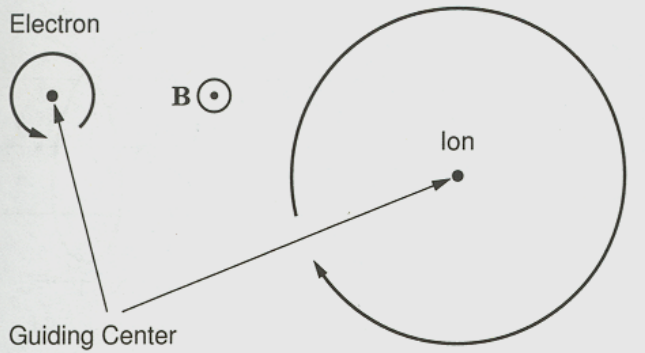
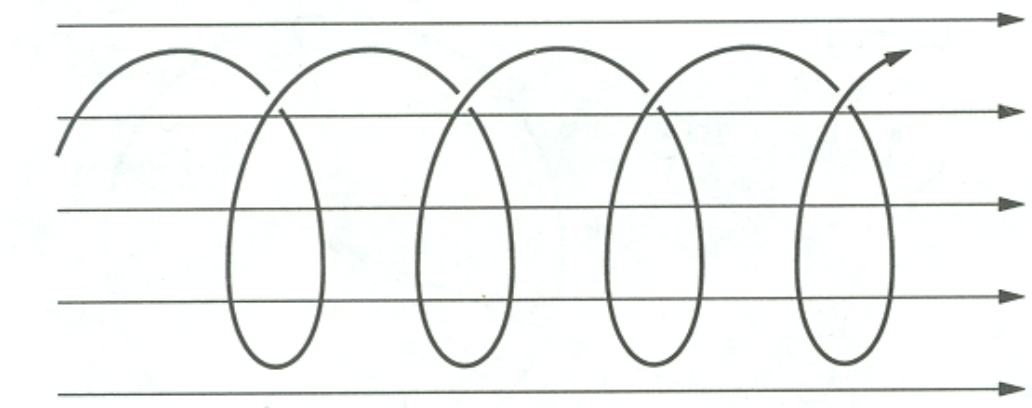
  • Single particle motion and Lorentz force \[ m\frac{d\vec{v}}{dt}=q\vec{v}\times\vec{B} \]
  • Gyro/cyclotron/Larmor-frequency \[ \Omega_c=\frac{qB}{m} \]
  • Gyro/Larmor-radius \[ \rho=\frac{|v_{\perp}|}{\Omega_c}=\frac{m|v_{\perp}|}{|q|B} \] (usually \(|v_{\perp}|=v_{th}\)).
  • Ratio of thermal to magnetic pressure. Plasma-\(\beta\) \[ \frac{nk_BT}{\frac{B^2}{2\mu_0}} \propto \left(\frac{\omega_{pe}}{\Omega_{ce}}\right)^2\left(\frac{v_{th}}{c}\right)^2. \]

4.6 Other relevant parameters

  • Thermal speed \[ v_{th} = \sqrt{\frac{k_bT}{m}} \]
  • Alfv'en speed \[ V_A = \frac{B}{\sqrt{\mu_0 n m_i}} \]
  • Ion skin depth/inertial length \[ d_i = \frac{c}{\omega_{pi}} = \frac{V_{A}}{\Omega_{ci}} \]

4.7 Plasma parameters

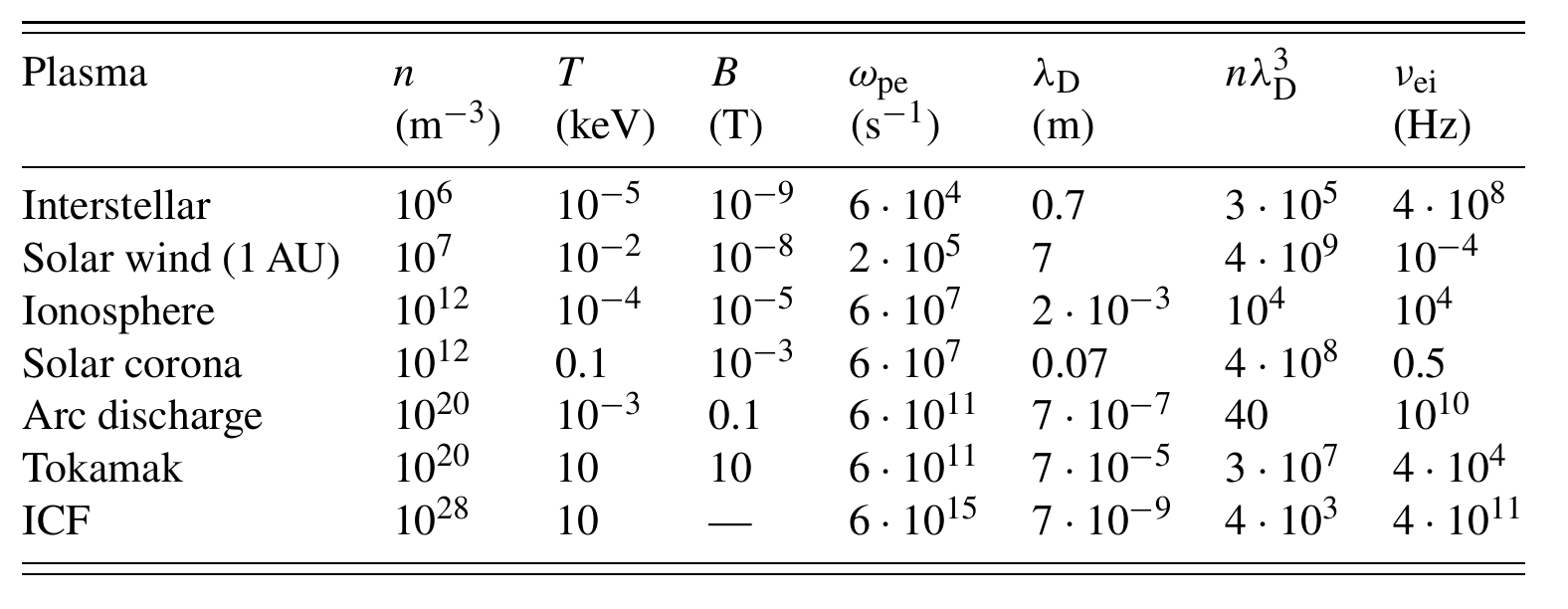
ICF = Inertial Confinement Fusion

(Boyd and Sanderson 2003)

4.8 Your turn

  1. Which main parameters can be used to describe a plasma?
  2. Select a parameter(s) and discuss its physical and intuitive meaning.
  3. What are approximative values of the plasma parameters in your favorite environment?

5 Plasma simulations

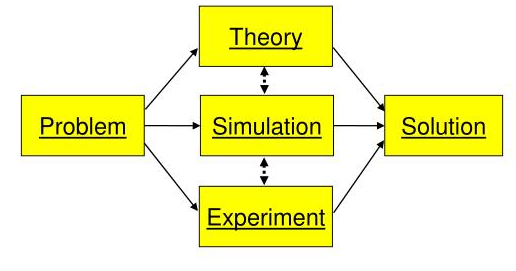
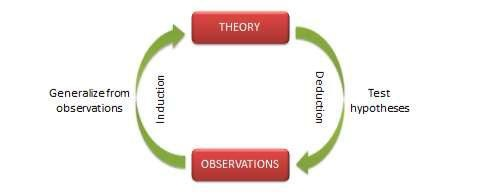
5.1 The role of simulations in science

5.2 Hierarchy of plasma physics models

Kinetic description

Microscopic properties, it uses the velocity distribution function \(f(\vec{x}, \vec{v}, t)\).

Fluid description

Uses a few macroscopic quantities, averages of the distribution function (mean velocity \(v(\vec{x},t)\), pressure/temperature). Valid for exact or near thermodynamic equilibrium.

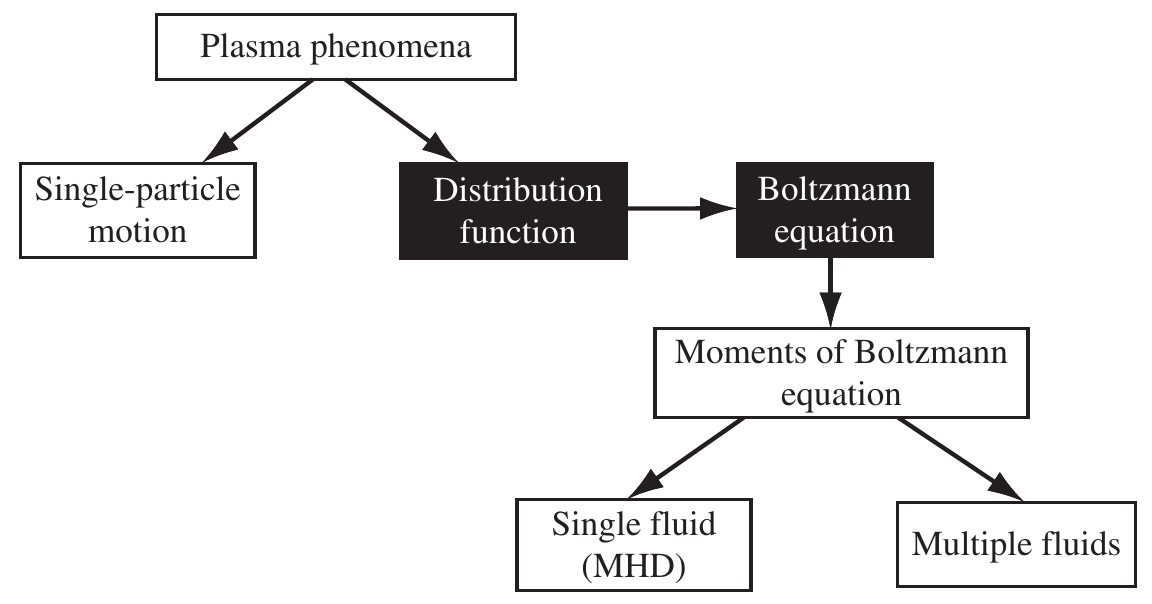
Hierarchy of plasma physics models

5.3 Validity of plasma models

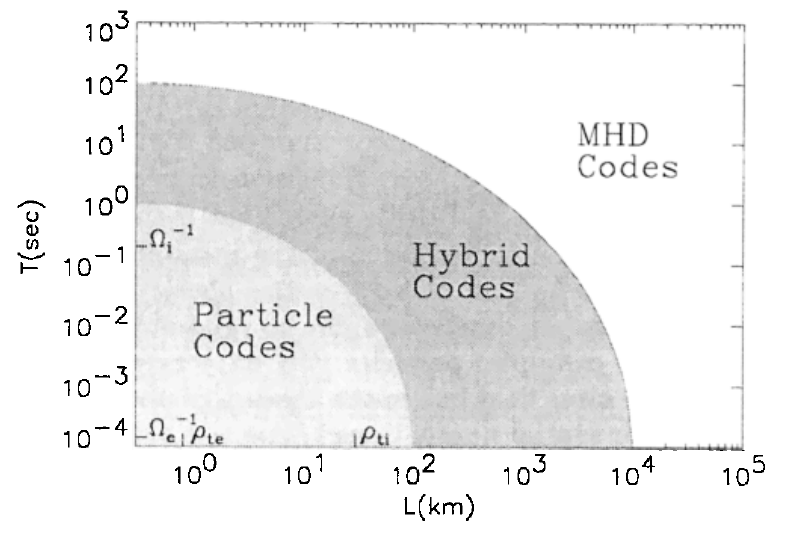
Range of validity of different plasma codes based on typical magnetospheric parameters: \(n=50cm^{-3}\), \(B=50 nT\), \(T_e=T_i=100 eV\) (Winske and Omidi 1996).

5.4 Validity of plasma models

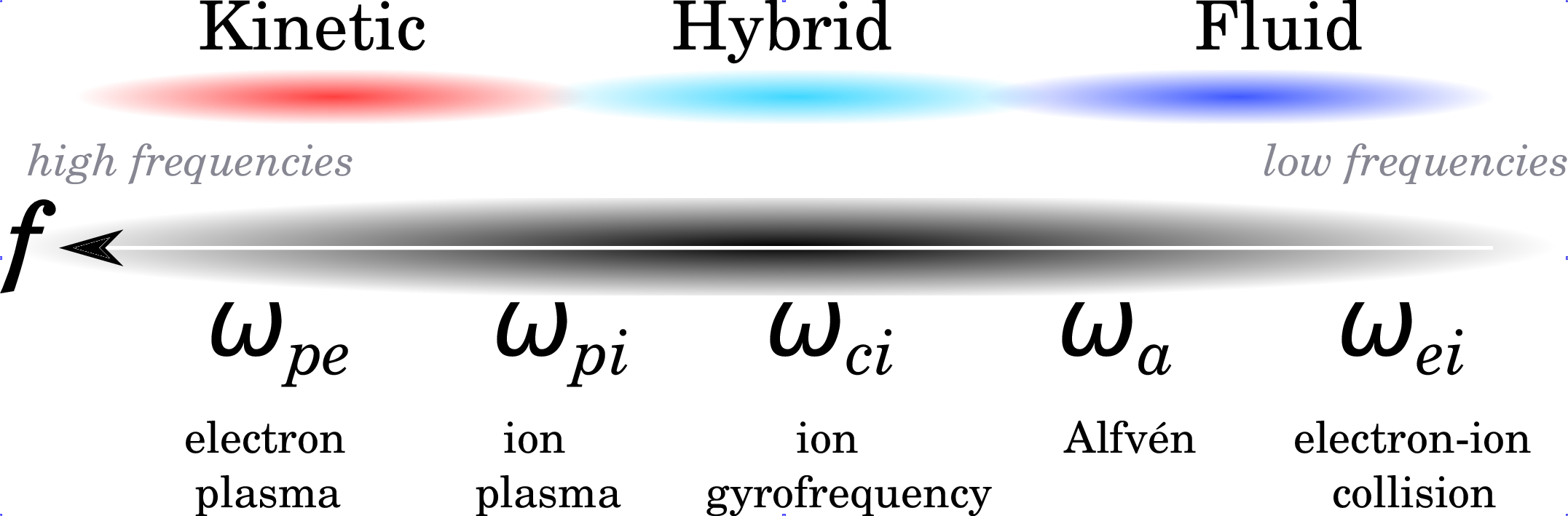Validity range of different plasma codes for a weakly collisional plasma [Credits: space.aalto.fi.]

5.5 Single-fluid MHD equations

Simplified single-fluid MHD equations (w/o explicit energy eq.)

\[ \nabla\cdot\vec{B}=0 \\ \nabla\times\vec{E}=-\frac{\partial \vec{B}}{\partial t} \nabla\times\vec{B}=\mu_0\vec{J} \\ \vec{E}+\vec{V}\times\vec{B}= \eta \vec{J}\\ \]

\[ \frac{\partial \rho}{\partial t} + \nabla(\rho\vec{V})=0 \\ \rho\frac{d\vec{V}}{dt} = \vec{J}\times\vec{B}-\nabla P\\ P=K\rho^{5/3} \]

5.6 Fully-kinetic/Vlasov description

Fully-kinetic equations

\[ \nabla\cdot\vec{E}=\frac{\rho}{\epsilon_0}\\ \nabla\cdot\vec{B}=0\\ \nabla\times\vec{E}=-\frac{\partial \vec{B}}{\partial t}\\ \nabla\times\vec{B}=\mu_0\vec{J}+\mu_0\epsilon_0\frac{\partial \vec{E}}{\partial t}\\ \]

\[ \left[\frac{\partial}{\partial t} + \vec{v}\cdot\frac{\partial}{\partial \vec{x}}+\frac{q_{\alpha}}{m_{\alpha}}\left(\vec{E}+\vec{v}\times\vec{B}\right)\cdot\frac{\partial}{\partial \vec{v}}\right]f_{\alpha}=0\\ \rho=\sum\limits_{\alpha} q_{\alpha}\int\limits dv^3\,f_{\alpha}\\ \vec{J}=\sum\limits_{\alpha} q_{\alpha}\int dv^3\,\vec{v}f_{\alpha} \]

5.7 Advantages and drawbacks of plasma simulations codes

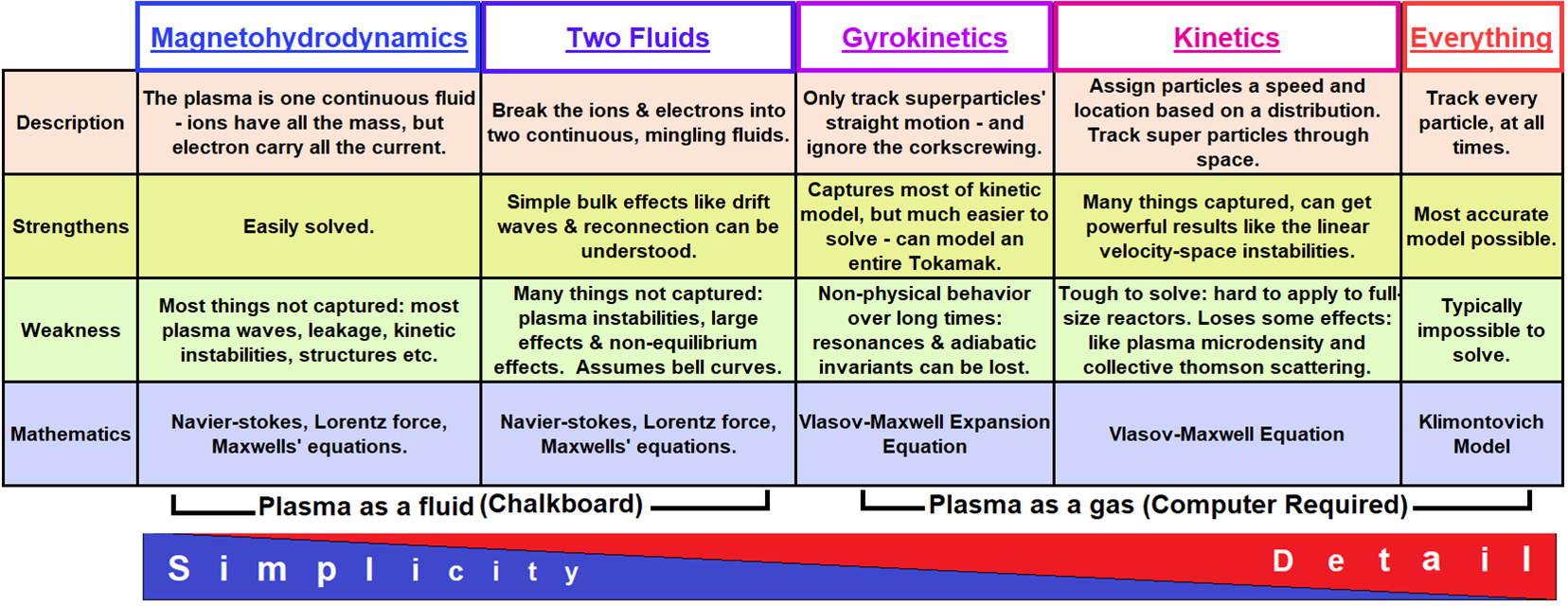
5.8 Your turn

  1. How would you characterize the relation between astronomical observations, theory, and simulations?
  2. Which example equations would use to describe the plasma?

6 Hands-on

6.1 Testing the computer setup

  1. Login to local computers using your student accounts
  2. Open command line
  3. Run Jupyter Notebook/Lab
  4. Load basic Python libraries Numpy and Matplotlib
  5. Plot an arbitrary analytical function (e.g., parabola, sin, cos,…)

If Jupyter Lab does not exist, run:

pip3 install --upgrade pip
pip3 install --user jupyterlab numpy scipy matplotlib
export PATH=$HOME/.local/bin:$PATH

OR

  • Instead of (1.–2.) Install and run Jupyter Lab on your computer.

7 Bibiography and references

7.1 Bibliography

  • Büchner (2023)
  • Büchner, Dum, and Scholer (2003)
  • Matsumoto and Omura (1993)
  • Jardin (2010)
  • Winske and Omidi (1996)
  • Lapenta (2012)
  • Umeda (2012)
  • Benáček et al. (2021)

7.2 References

Benáček, Jan, Patricio A. Muñoz, Alina C. Manthei, and Jörg Büchner. 2021. “Radio Emission by Soliton Formation in Relativistically Hot Streaming Pulsar Pair Plasmas” 915 (2): 127. https://doi.org/10.3847/1538-4357/ac0338.
Boyd, T. J. M., and J. J. Sanderson. 2003. The Physics of Plasmas.
Büchner, Jörg. 2023. Space and Astrophysical Plasma Simulation. Methods, Algorithms, and Applications. https://doi.org/10.1007/978-3-031-11870-8.
Büchner, Jörg, C Dum, and M Scholer. 2003. Space Plasma Simulation. Berlin Heidelberg: Springer-Verlag.
Jardin, S. 2010. Computational Methods in Plasma Physics. CRC Press.
Lapenta, Giovanni. 2012. “Particle simulations of space weather.” J. Comput. Phys. 231 (3): 795–821. https://doi.org/10.1016/j.jcp.2011.03.035.
Matsumoto, H, and Y Omura. 1993. Computer Space Plasma Physics : Simulation Techniques and Software. Terra Scientific Publishing Company. https://www.terrapub.co.jp/e-library/cspp/.
Umeda, Takayuki. 2012. “Simulation of Collisionless Plasma With the Vlasov Method.” In Int. Conf. Simul. Technol., edited by Brian S. Doherty and Amy N. Molloy, 315–32. Nova Science Publishers. http://www.jsst.jp/e/JSST2012/extended_abstract/pdf/12.pdf.
Winske, D., and N. Omidi. 1996. “A nonspecialist’s guide to kinetic simulations of space plasmas.” J. Geophys. Res. 101 (A8): 17287. https://doi.org/10.1029/96JA00982.