Lecture 4: Testing particle – hands-on

Jan Benáček

Institute for Physics and Astronomy, University of Potsdam

November 9, 2023

Table of contents

• Lecture overview
• 1 Particle drifts/guiding center
• 2 Test particle algorithms
• 3 Hands-on

Lecture overview

Table of Contents 1/2

• 19.10. Introduction + numerical methods summary
• 26.10. Numerical methods for differential equations - lecture + hands-on
• 02.11. Test particle approach — lecture
• 09.11. Test particle approach — hands-on
• 16.11. PIC method — lecture
• 23.11. PIC method — hands-on
• 30.11. Fluid and MHD — lecture

Table of Contents 2/2

• 07.12. Fluid and MHD — hands-on
• 14.12. Radiative transfer — lecture
• 11.01. Radiative transfer — hands-on
• 18.01. HPC computing — lecture + hands-on
• 25.01. Advanced — Smooth particle hydrodynamics method — lecture
• 01.02. Advanced — Hybrid, Gyrokinetics — lecture
• 08.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture

1 Particle drifts/guiding center

1.1 Particle drifts/guiding center

1.2 Particle motion in background magnetic fields

• The basic motion of a particle under the influence of a static and uniform magnetic field is the gyromotion.
• Taking the dot product of Equation (13) from the last lecture with \(\vec{v}\), we get \[ \frac{d}{dt}\left(\frac{mv^2}{2}\right) = 0. \] That is, a static magnetic field cannot change the kinetic energy of a particle.

1.3 Particle motion in background magnetic fields

• Assuming a magnetic field \(\vec{B}=B\hat{z}\), the equation becomes: \[ m\frac{dv_x}{dt}=qB v_y\\ m\frac{dv_y}{dt}=-qB v_x\\ m\frac{dv_z}{dt}=0 \] and thus, \[ \frac{d^2v_x}{dt^2} + \Omega_c^2 v_x=0\\ \frac{d^2v_y}{dt^2} + \Omega_c^2 v_y=0 \]

1.4 Particle motion in background magnetic fields

• Where the gyrofrequency (or Larmor/cyclotron) is: \[ \Omega_c=\frac{qB}{m} \]
• Solution \[ v_x = v_{\perp}\cos\left( \Omega_c t + \psi \right) \\ v_y = v_{\perp}\sin\left( \Omega_c t + \psi \right) \\ v_z=v_{\parallel} \] where \(\psi\) is an arbitrary phase angle.
• By integrating we get, \[ x = \rho_c\sin\left( \Omega_c t + \psi \right) + (x_0 - r_c\sin\psi) \\ y = -\rho_c\cos\left( \Omega_c t + \psi \right) + (y_0 + r_c\cos\psi) \\ z=z_0 + v_{\parallel}t \qquad(1)\]

1.5 Particle motion in background magnetic fields

• Where the gyroradius (or Larmor radius or cyclotron radius) is: \[ \rho_c=\frac{|v_{\perp}|}{\Omega_c}=\frac{m|v_{\perp}|}{|q|B} \] Note that this can be understood from force balancing the “centrifugal” force: \[ \frac{mv_{\perp}^2}{r}=qv_{\perp}B \]
• Particles move in circular/helical orbits with frequency \(\Omega_c\) and radius \(\rho_c\) about the guiding center \[ R_g=\hat{x}x_0 + \hat{y}y_0 + \hat{z}(z_0 + v_{\parallel}t) \]
• Note that particles with higher velocities orbit in circles with larger radii, but the same frequency.
• Particles with larger masses orbit in circles with larger radii, but with lower frequencies (longer periods).

1.6 Particle motion in magnetic fields (helical motion)

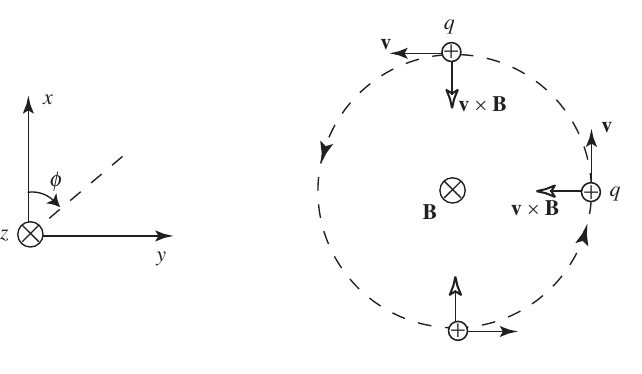
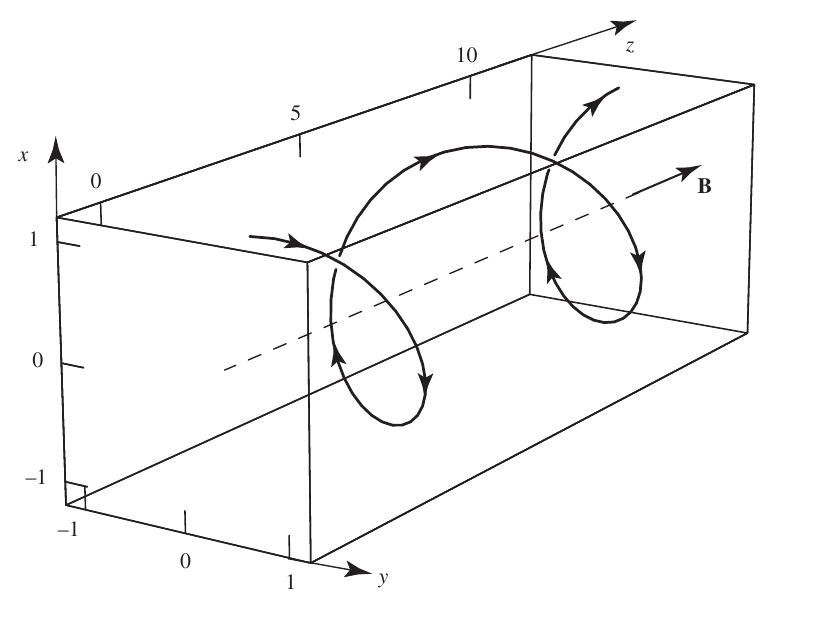
1.7 Particle motion in background magnetic fields

• Pitch angle: \[ \alpha=\tan^{-1}\left(\frac{v_{\perp}}{v_{\parallel}}\right) \]
• Magnetic moment \[ \mu=\underbrace{\frac{q\Omega_c}{2\pi}}_{\text{current}}\underbrace{\pi \rho_c^2}_{\text{area}}=\frac{mv_{\perp}^2}{2B} \]
• The direction of the magnetic field generated by the gyration is opposite to that of the external field: a plasma is a diamagnetic medium.

1.8 \(\vec{E}\times\vec{B}\) drift

• Let us consider, in addition to \(\vec{B}=\hat{z}B\), an electric field:
  \(\vec{E}=\hat{x}E_{\perp} + \hat{z}E_{\parallel}\). The equations of motions are: \[ \label{ecross1} m\frac{d\vec{v}_{\perp}}{dt}=q(\hat{x}E_{\perp} + \vec{v}_{\perp}\times \hat{z}B)\\ m\frac{dv_{\parallel}}{dt}=qE_{\parallel} \qquad(2)\]
• Let us decompose \(\vec{v}_{\perp}=\vec{v}_E + \vec{v}_{ac}\). By choosing: \[ \vec{v}_E=\frac{\vec{E}\times\vec{B}}{B^2} \]
• Equation 2 becomes the eq. for gyration with frequency \(\Omega_c\). \[ m\frac{d\vec{v}_{ac}}{dt}=q\vec{v}_{ac}\times\hat{z}B \]
• The solution is then: \[ \vec{v}(t)=\hat{z} v_{\parallel}(t) + \vec{v}_E + \vec{v}_{ac}(t) \]

1.9 \(\vec{E}\times\vec{B}\) drift

• The average of \(\vec{v}\) over one gyroperiod is: \[ \langle \vec{v} \rangle = \hat{z} v_{\parallel} + \vec{v}_E \] so \(\vec{v}_E\) is the average perpendicular velocity.
• This drift arises from the difference in the local gyroradius between top/bottom.
• The \(\vec{E}\times\vec{B}\) drift is independent on \(q\), \(m\) and \(v_{\perp}\).

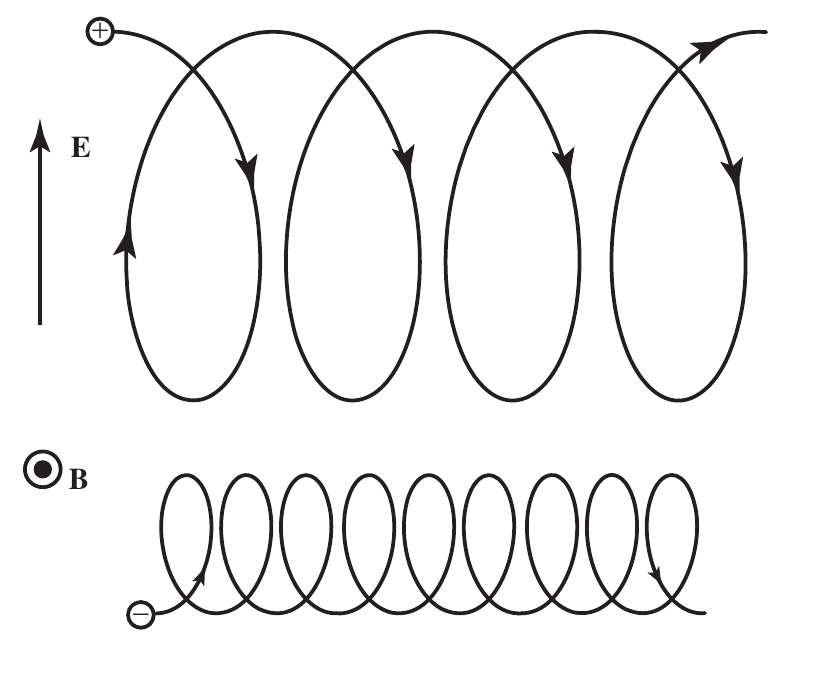
1.10 Gradient B drift

• Let us assume a magnetic field with intensity varying in the perpendicular direction to the B-vector \(\vec{B}(y)=\hat{z}B_z(y)\).
• This drift also arises from a force perpendicular to the magnetic field. Generalizing the expression for the \(\vec{E}\times\vec{B}\) force: \[ \vec{v}_F=\frac{\left( \frac{\vec{F}_{\perp}}{q} \right) \times\vec{B}}{B^2} \]

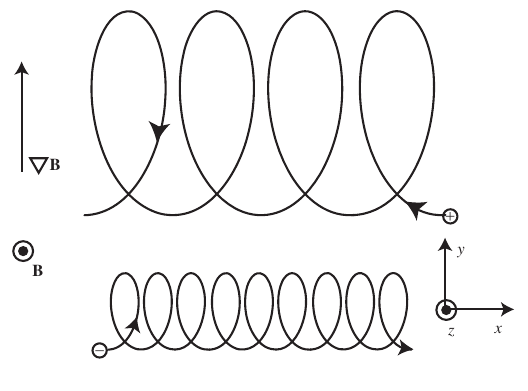
1.11 Gradient |B| drift

• In this geometry, the perpendicular force is \[ \vec{F} = q\vec{v}\times\vec{B}=\hat{x}qv_yB_z - \hat{y}qv_xB_z \sim \hat{x}qv_y\left(B_0 + y\frac{\partial B_z}{\partial y} \right)-\hat{y}qv_x\left(B_0 + y\frac{\partial B_z}{\partial y} \right) \]
• By assuming that particles follow approximately orbits in an uniform field (Equation 1), we can determine the gyroaverage force \(\vec{F}\): \[ \langle F_y \rangle = \frac{q v_{\perp} r_c}{2}\frac{\partial B_z}{\partial y}=\frac{m v_{\perp}^2}{2B}\frac{\partial B_z}{\partial y}\hspace{0.5cm}\text{or more generally}\hspace{0.5cm}=\frac{W_{\perp}}{B}\nabla |\vec{B}| \]
• This way, the grad-B (\(\nabla \vec{B}\)) drift velocity is: \[ \vec{v}_{\nabla B} = \frac{ \left( \frac{\vec{F}_{\perp}}{q} \right)\times\vec{B}}{B^2}=\frac{\langle\vec{F_y}\rangle\hat{y}\times\hat{z}B_z}{qB_z^2} = \frac{mv_{\perp}^2}{2qB_z}\frac{\partial B_z}{\partial y}\hat{x} \] or more generally \[ \vec{v}_{\nabla B} = \frac{mv_{\perp}^2}{2q}\frac{\vec{B}\times\nabla B}{B^3} \]

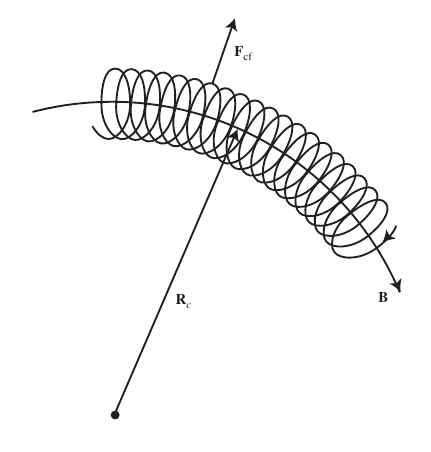
1.12 Curvature B drift

• In a curved magnetic field line, particles experience a centrifugal force perpendicular to the B-field \[ \vec{F}_{cf}=mv_{\parallel}^2\frac{\vec{R}_c}{R_c^2} \] which causes a drift perpendicular to both vectors.

1.13 Curvature B drift

• Curvature drift: \[ \vec{v}_{R} = \frac{ \left( \frac{\vec{F}_{cf}}{q} \right) \times\vec{B}}{B^2}= \frac{mv_{\parallel}^2}{q}\frac{\vec{R}_c\times\vec{B}}{R_c^2 B^2} \]
• In vacuo this drift cannot be the only one because \(\nabla\times \vec{B} = 0\). A more general expression due to both gradient and curvature drifts is: \[ \vec{v}_{total}=\vec{v}_{R} + \vec{v}_{\nabla} =\left(v_{\parallel}^2 + \frac{v_{\perp}^2}{2} \right)\frac{\vec{B}\times\nabla B}{\Omega_c B^2} \]

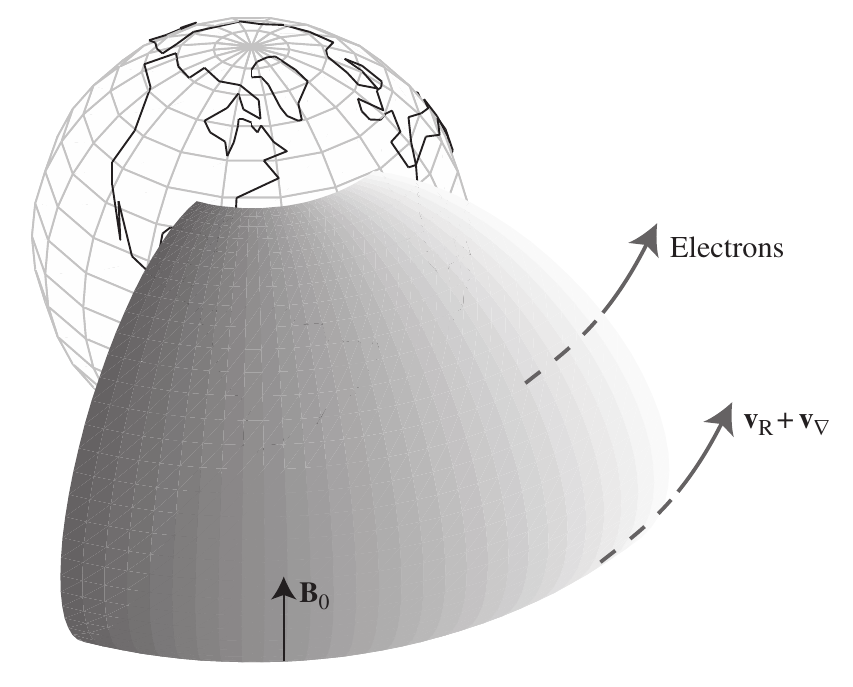
1.14 Curvature B drift

• Longitudinal drift of radiation belt electrons (and associated ring current because of opposite ion/electron drift)

1.15 Adiabatic invariance of the magnetic moment

• Magnetic moment \(\mu=\frac{mv_{\perp}^2}{2B}\) tends to be conserved as long as (spatial or temporal) changes in B are small over a gyroradius or gyroperiod.
• The particle’s perpendicular energy increases while its parallel energy decreases as it moves toward regions of stronger B, until it eventually \(v_{\parallel}=0\) and it bounces back (magnetic mirror/bottle).

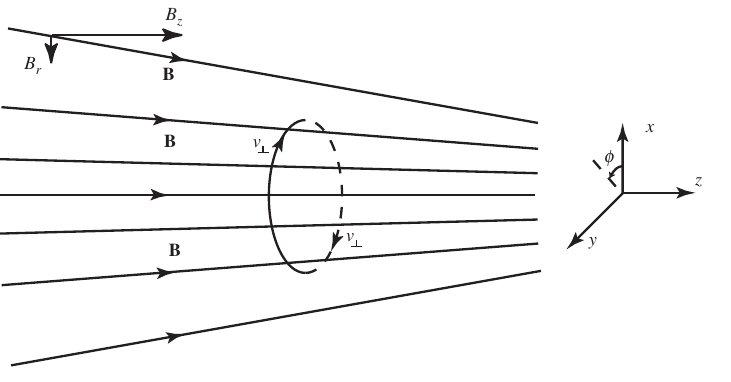
1.16 Particle trajectories in the Earth’s magnetosphere

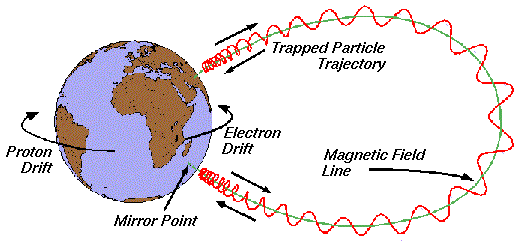
Credits: Spenvis (ESA’s SPace ENVironment Information System) Models description

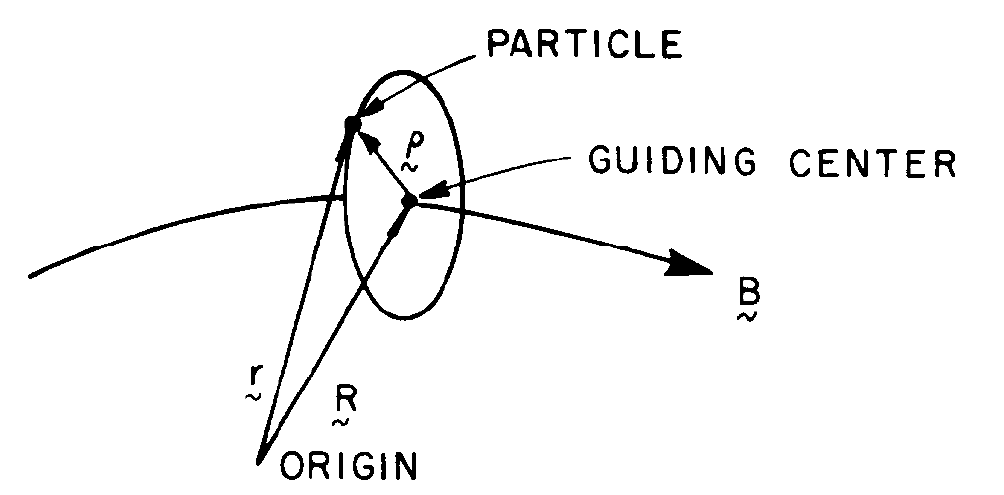
1.17 Guiding center approximation

• Valid when the gyroradius (\(\rho= \frac{mv}{qB}\)) and gyroperiod (\(\propto \frac{1}{\Omega} = \frac{m}{qB}\)) are much smaller than the length scale of transverse gradients and characteristic oscillation periods of the background EM fields.

• The motion of a charged particle is described in terms of variables representing the gyration around B-field lines and the motion of its guiding center.

• For the solar corona, typical gyroradii are \(10^{-3} m\) for electrons and \(10^{-2} m\) for protons, much smaller than typical characteristic lengths scales.

2 Test particle algorithms

2.1 Test particle algorithms

2.2 Method 1: trajectory sampling

• It solves individual representative trajectories (the choice is not trivial)
• Useful to visualize aspects such as particle transport or energetics

2.3 Method 2: Forward Monte Carlo

• Inject (randomly) particles in source regions where \(f\) is known, and follow them until they reach the regions of interest. Injected particles are tagged with a statistical weight \(w_i\) based on the number of injected particles per time \(\Gamma_{MC}\) and the physical flux \(\Gamma_{Phys}\): \[ w_i=\frac{\Gamma_{Phys}}{\Gamma_{MC}} \]
• Statistical analysis of particles via sampling (binning) in \(x\) and \(v\) space (which implies large statistical errors), and using \(w_i\). For instance: \[ n=\frac{1}{\Delta x^3}\sum_i^N w_i \\ \Gamma_x=\frac{1}{\Delta x^3}\sum_i^N v_{ix}w_i \\ f(\vec{x},\vec{v})=\frac{1}{\Delta x^3\Delta v^3}\sum_i^N w_i \]
• It is the most similar approach to the PIC method, but in this case with not self-consistent fields.

3 Hands-on

3.1 MHD simulation of magnetic reconnection (plasmoid/long current sheet)

• Physical model: Resistive MHD + subgrid-scale turbulent model.
• Parameters applied to Mercury’s magnetotail
• Details in Zhou et al., 2018, also at https://arxiv.org/abs/1806.10665

3.2 Simple python code

1. Read electromagnetic field data from MHD simulation snapshot (grid: 12802x 3202)
2. Compute supplementary fields (like current density)
3. Calculate electromagnetic fields at particles’ position (interpolation)
4. Integrate particles using Lorentz force (or guiding center approximation) eq via Runge-Kutta 4th order (TODO: Boris pusher)
5. Diagnostics (plots)

• Normalizations, \(t_0 = 1s, B_0 = 7.5 \times 10^{-8} T , L_0 = 2.5 \times 104\) m, \(\beta p = 0.5\)
• Integration parameters: \(dt = 0.13 \Omega_{ce}^{-1} (10^{-5} t_0 ), t_{max} = 3 t_0 > 100\) electrons.

3.3 Tasks

Important: Memory limit of 16GB per instance.

• Exercise 1: Compute electron trajectories on the current sheet and plasmoids.
• Exercise 2: Determine particle energization as a function of time. And locations where it occurs.
• Exercise 3: Using the guiding center approximation, determine the main contributions to the particle energization (in terms of particle drifts).

You can download the Jupyter notebook here: https://www.app.physik.uni-potsdam.de/~jbenacek/ASPS/lecture04-handson.ipynb