Lecture 3: Test particles – lecture

Jan Benáček

Institute for Physics and Astronomy, University of Potsdam

November 7, 2024

Table of contents

• Lecture overview
• 1 Partial differential equations
• 2 Introduction to testing particle method
• 3 Integration of particle trajectories

Lecture overview

Table of Contents 1/2

• 17.10. Introduction + numerical methods summary
• 24.10. Numerical methods of differential equations — lecture + hands-on
• 31.10. State holiday
• 07.11. Test particle approach — lecture
• 14.11. Test particle approach — hands-on
• 21.11. PIC method — lecture
• 28.11. PIC method — hands-on

Table of Contents 2/2

• 05.12. Fluid and MHD — lecture
• 12.12. Canceled
• 19.12. Fluid and MHD — hands-on
• 09.01. Radiative transfer — lecture + hands-on
• 16.01. HPC computing — lecture + hands-on
• 23.01. Advanced — Smooth particle hydrodynamics method — lecture
• 30.01. Advanced — Hybrid, Gyrokinetics — lecture
• 06.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture

1 Partial differential equations

Finishing from previous lecture

1.1 Characteristics of PDEs

• Curves in the space of independent variables of a PDE, along which the PDE has only total differentials.

  By integrating along those curves one can find the solutions of such a PDE.

• Example: \[ a\frac{\partial u}{\partial t} + b\frac{\partial u}{\partial x} = c \] with solutions \(u=u(x(t),t)\).

• Total derivative of \(u\): \[ \frac{du}{dt}=\frac{\partial u}{\partial x}\frac{dx}{dt} + \frac{\partial u}{\partial t} \]

• The characteristics are the solutions of: \[ \frac{dx}{dt}=\frac{b}{a},\;\; \frac{du}{dt}=\frac{c}{a} \] which means, for \(u(x_0,0)=u_0\), \[ x = x_0 + \frac{b}{a}t\\ u = u_0 + \frac{c}{a}t\\ \]

1.2 Characteristics of PDEs

• Curves in the space of independent variables of a PDE, along which the PDE has only total differentials
• Solution/characteristics: \[ x = x_0 + \frac{b}{a}t\\ u = u_0 + \frac{c}{a}t\\ \]
• Note that if \(c=0\), \(u\) is constant on the characteristics.
• For non constant \(c\), \(u\) grows linearly in time along a characteristic \(\Rightarrow\) the initial profile \(u(x,0)\) already determines the solution along the characteristics

1.3 Characteristics of PDEs

• For the second order PDE: \[ A\frac{\partial^2 f}{\partial x^2} + B\frac{\partial^2 f}{\partial x \partial y} + C\frac{\partial^2 f}{\partial y^2} + G = 0 \]

The characteristics are the solutions of: \[ \frac{dy}{dx} = \frac{B}{2A}\pm \frac{1}{2A}\sqrt{B^2 - 4AC} \]

This equation is:

• elliptic: \(B^2 - 4AC < 0\). No real solutions.
• parabolic if \(B^2 - 4AC = 0\). One real solutions.
• hyperbolic if \(B^2 - 4AC > 0\). Two real solutions.

1.4 Systems \(n\) of 1st order PDEs

• It is possible to write such a system of \(n\) PDEs in two dependent variables \(x\) and \(y\) as: \[ \left(\bar{A}^T\frac{dy}{dx} - \bar{B}^T \right)\cdot \vec{L} = 0 \] where \(\vec{L}\) is a vector of dimension \(n\), \(\bar{A}^T\), \(\bar{B}^T\), are \(n\times n\) matrices.

  The determinant leads to a \(n\)th order equation for \(dy/dx\), which can be classified as:

  • elliptic for no real roots
  • parabolic for \(1\) to \(n-1\) real roots and no complex roots
  • hyperbolic for \(n\) real roots

1.5 Classification

1.6 Linear Second Order PDEs in 2 independent variables

• The most general form of a linear second order PDE with independent variables \(x,y\) and dependent variable \(f(x,y)\) is: \[ A\frac{\partial^2 f}{\partial x^2} + B\frac{\partial^2 f}{\partial x \partial y} + C\frac{\partial^2 f}{\partial y^2} + D\frac{\partial f}{\partial x} + E\frac{\partial f}{\partial y} + G = 0 \]

  \(A,\dots, G\) are constants.

This equation is:

• elliptic if \(B^2 - 4AC < 0\)

• parabolic if \(B^2 - 4AC = 0\)

• hyperbolic if \(B^2 - 4AC > 0\)

1.7 Linear Second Order PDEs in 2 independent variables

\[ A\frac{\partial^2 f}{\partial x^2} + B\frac{\partial^2 f}{\partial x \partial y} + C\frac{\partial^2 f}{\partial y^2} + D\frac{\partial f}{\partial x} + E\frac{\partial f}{\partial y} + G = 0 \]

• Elliptic (\(B^2 - 4AC < 0\)): Steady state problems (gravity, electrostatic). Laplace equation (2D): \[ \nabla ^2\phi = \frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} =0 \]
• Parabolic (\(B^2 - 4AC = 0\)): Time-dependent fluid equations where conduction/diffusion are important. Heat conduction equation \[ \frac{\partial T}{\partial t}=k\frac{\partial^2 T}{\partial x^2} \]
• Hyperbolic ( \(B^2 - 4AC > 0\)): Time-dependent fluid eqs where convection is important. Vibration, propagation. Wave equation \[ \frac{\partial^2U}{\partial t^2}=c^2\frac{\partial^2 U}{\partial x^2} \]

1.8 Multiple independent variables

• Let us consider a single dependent variable \(f\) but \(m\) independent variables: \[ \sum_{j=1}^{m} \sum_{k=1}^{m} a_{jk} \frac{\partial^2 f}{\partial x_j \partial x_k} + H=0 \] The character of this eq is determined by the eigenvalues (EV) of the matrix \(A=(a_{jk})\).
• This equation is
  • elliptic if all the EVs \(\neq0\) and all the same sign.
  • parabolic if any EV is 0
  • hyperbolic if all the EVs \(\neq0\) and all but one have the same sign.

1.9 Your turn

• Which kind of differential equation is:
  • Lorentz force
  • Schrödinger equation
  • Maxwell equations

1.10 Elliptic PDEs

• Typical for steady state problems (time-independent limit of hyperbolic or parabolic eqs), or for potentials (Poisson’s equation).
• Example: 2D Poisson equation (Or Laplace’s equation if the RHS=0) \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \rho(x,y) \qquad(1)\]
• Solution for 4 boundary conditions: \[ u(x,y) = \sin(\pi x)\exp(-\pi y) \]
• No real characteristics
• Both the maximum and minimum are assumed on the boundary \(\partial R\).
• Any disturbance on the interior influences the entire computational domain.

1.11 Parabolic PDEs

• Example: heat conduction, magnetic flux diffusion, evolution of a velocity distribution function in velocity space due to particle collisions. \[ \frac{\partial u}{\partial t}= \sigma \frac{\partial^2 u}{\partial x^2} \qquad(2)\]
• Solution for one initial condition (typically Dirichlet) and two boundary conditions: \[ u(x,t) = \sin(\pi x)\exp(-\pi^2 t) \]
• Only one characteristic
• Any local perturbation influences the entire domain, but with decreasing magnitude for increasing distance from the source of the perturbation.

1.12 Hyperbolic PDEs

• Example: wave equation: \[ \frac{\partial^2 u}{\partial t^2} - c^2\frac{\partial^2 u}{\partial x^2} = 0 \qquad(3)\]
• Solution: Two sine waves, traveling into the positive (\(+x\)) and negative (\(-x\)) directions.
• Typical property: propagation of information through a system via waves (e.g. sound waves) along the characteristics of the equation.
• Examples: various time dependent forms of fluid equations without dissipation: heat conduction, viscosity, resistivity
• The number of initial conditions (this case: dependent variables and their derivatives) has to correspond with the number of unknowns or waves.
• Any point source along \(x\) will influence its vicinity along the corresponding characteristics (two straight lines for Eq. Equation 3.

1.13 Hyperbolic PDEs

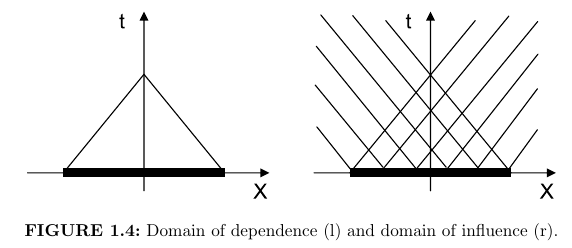
Characteristics of a hyperbolic wave equation. Left: Domain of dependence. Right: Domain of influence (Jardin (2010)).

1.15 Boundary conditions

Let us define a domain, its boundary \(\partial R\), the coordinates \(n\) (outward normal to the boundary) and \(s\) (along the boundary), and the functions \(f\) and \(g\) on the boundary. The three types of BCs are:

1. Dirichlet conditions: \(u=f\) on \(\partial R\)
2. Neumann conditions: \(\frac{\partial u}{\partial n} =f\) or \(\frac{\partial u}{\partial s} =g\) on \(\partial R\)
3. Mixed (Robin) conditions: \(\frac{\partial u}{\partial n} + ku=f, \;\; k>0\) on \(\partial R\).

1.16 Initial vs Boundary conditions

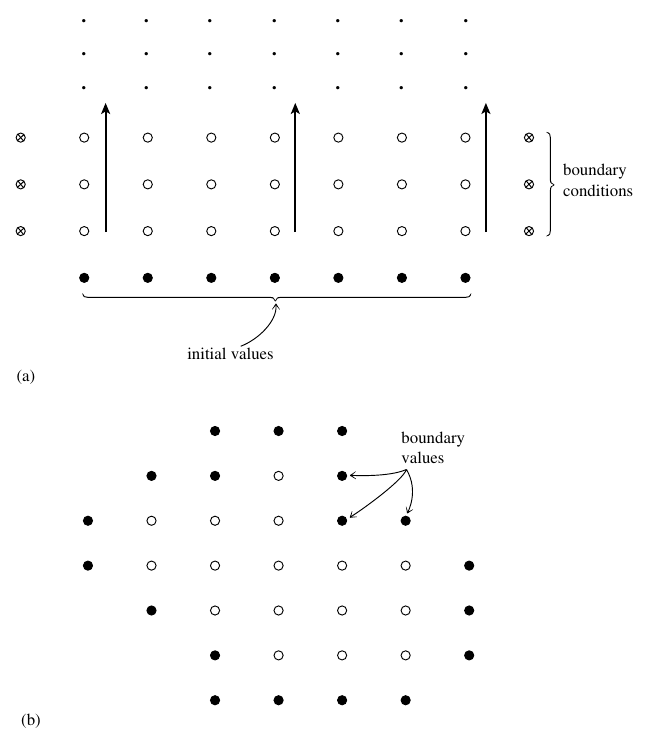
(a) Initial (Cauchy) vs (b) Boundary value problems (Press et al. (2007)). In (a) the arrows indicate time.

1.17 Stability

1.18 Von Neumann stability analysis

• Based on a finite Fourier transform to convert spatial differences into an expression with the \(\xi\), such as the independent solutions (eigenmodes) are: \[ u_j^n=\xi^n(k) e^{ikj\Delta x} \qquad(4)\] \(j\) is the space index, \(n\) is the time index, \(i\) the imaginary unit, \(k\) the wavenumber, \(\Delta x\) the grid cell spacing.
• The difference equation will be unstable if \(|\xi(k)|>1\) for some \(k\). This means exponential growing modes.
• von Neumann analysis is local.

1.19 Von Neumann stability analysis 2

• Example: numerically unstable hyperbolic equation: wave equation written as a system of 1st order equations (each one is sometimes called “advective equations”). \[ \frac{\partial u}{\partial t} = -v \frac{\partial u}{\partial x} \] The (forward time centered space) FTCS representation is: \[ \frac{u_j^{n+1} - u_j^{n}}{\Delta t} = -v \left(\frac{u_{j+1}^{n} - u_{j-1}^{n}}{2\Delta x} \right) \qquad(5)\]
• Replacing Equation 4 in Equation 5 we get: \[ \frac{\xi^{n+1}(k)}{\xi^n(k)}=1-i\frac{v\Delta t}{\Delta x}\sin(k\Delta x) \] which is \(|\frac{\xi^{n+1}(k)}{\xi^n(k)}|>1\) for all \(k\), so that the scheme is unstable.

1.20 Von Neumann stability analysis 3

• Example: numerically stable hyperbolic equation: let us replace the time derivative in Equation 5 by its average: \[ u_j^{n+1} = \frac{1}{2}\left(u_{j+1}^{n} + u_{j-1}^{n}\right) -\frac{v\Delta t}{2\Delta x} \left(u_{j+1}^{n} - u_{j-1}^{n} \right) \qquad(6)\] (this is known as the Lax method), which gives the amplification factor: \[ \xi(k)=\cos(k\Delta x)-i\frac{v\Delta t}{\Delta x}\sin(k\Delta x) \] and it leads to the stability condition (under the assumption that \((k\Delta x) < 1\)):

Courant-Friedrichs-Lewy

Courant-Friedrichs-Lewy stability condition (CFL, Courant condition): \[ \frac{v\Delta t}{\Delta x}\leq 1 \] Example: 2nd order hyperbolic wave equation (derived from the determinant of a matrix).

1.21 CFL condition

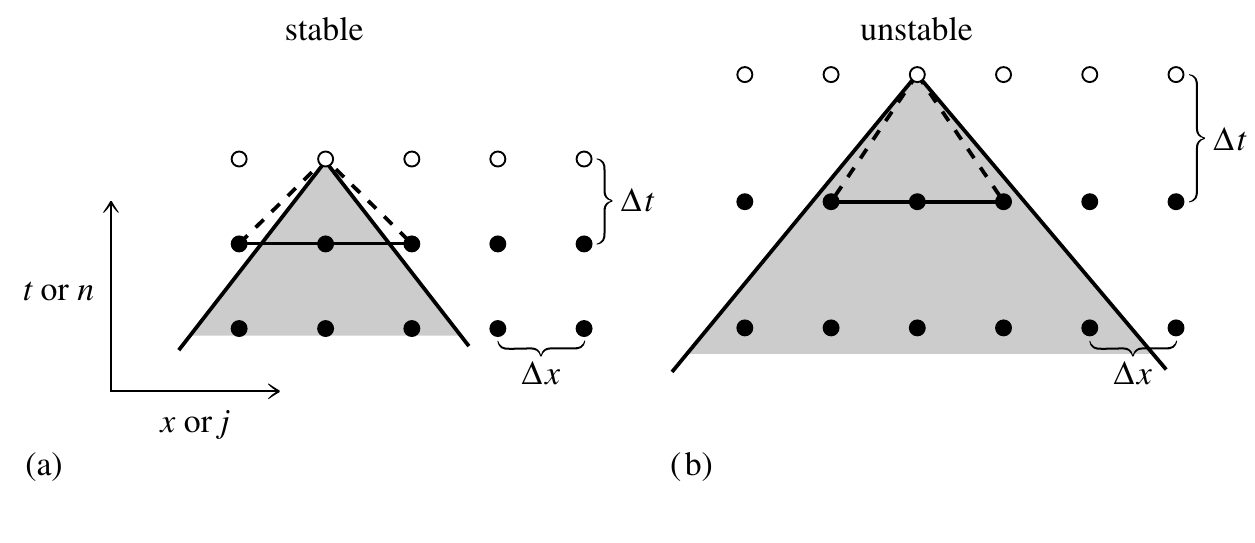
CFL condition (Jardin (2010)).

1.22 Von Neumann stability analysis 4

• It can be proven that Equation 6 is equivalent to a FTCS (forward time-centered space) representation of \[ \frac{\partial u}{\partial t} = -v \frac{\partial u}{\partial x} + \frac{(\Delta x)^2}{2\Delta t}\nabla^2 u \] where the extra term is a diffusion/dissipative term. Then, the Lax scheme is said to have numerical dissipation or viscosity.

1.23 Methods

1.24 Solution methods for parabolic equations 1

• Diffusion equation in 1D \[ \frac{\partial u}{\partial t}= D \frac{\partial^2 u }{\partial x^2} \qquad(7)\] where \(D\) is the diffuction parameter.

  This can also be written as a flux-conservative equation, with F=-\(D \frac{\partial u}{\partial x}\).

• \(D\geq 1\) in order for Eq. Equation 7 to be stable.

• Applying a FTCS scheme we get: \[ \frac{u_j^{n+1} - u_j^{n}}{\Delta t} = D \left(\frac{u_{j+1}^{n} -2u_j^n + u_{j-1}^{n}}{(\Delta x)^2} \right) \qquad(8)\]

1.25 Solution methods for parabolic equations 2

• The amplification factor is: \[ \xi(k)=1 -\frac{4D \Delta t}{(\Delta x)^2}\sin(k\Delta x/2) \] leading to the stability criterion: \[ \frac{2D\Delta t}{\Delta x}\leq 1 \qquad(9)\] the maximum allowed timestep is approx. the diffusion time across a cell of width \(\Delta x\).
• In general, the diffusion time across a spatial scale of size \(\lambda\) is \(\tau\sim \frac{\lambda^2}{D}\), which leads to a number of timesteps (based on Equation 9) of order \(\frac{\lambda^2}{\Delta x^2}\) \(\rightarrow\) too many.

1.26 Solution methods for parabolic equations 3

• One solution to change the small CFL timestep of the diffusion eq. is the Crank-Nicholson scheme, second-order accurate in time.
• Average of explicit and implicit FTCS schemes: \[ \frac{u_j^{n+1} - u_j^{n}}{\Delta t} = \frac{D}{2}\left(\frac{(u_{j+1}^{n+1} -2u_j^{n+1} + u_{j-1}^{n+1}) +(u_{j+1}^{n} -2u_j^{n} + u_{j-1}^{n}) }{(\Delta x)^2} \right) \qquad(10)\]
• The amplification factor predicts that the method is stable for any \(\Delta t\)
• Crank-Nicholson also works well for Schrödinger-like eqs. \[ i\frac{\partial \psi}{\partial t} = -\frac{\partial ^2\psi}{\partial x^2} + V(x)\psi \]

1.27 Solution methods for elliptic PDEs

• 2D Poisson equation \[ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = R(x,y) \qquad(11)\] with Dirichlet boundary conditions: \[ u(0,y), u(L,y) \qquad 0<y<L \] and \[ u(x,0), u(x,L) \qquad 0<x<L \]

The 2nd order finite difference equation for \(j,k\)-element (derived by the Taylor expansion) is: \[ u_{j+1,k} + u_{j-1,k} + u_{j,k+1} + u_{j,k-1} - 4u_{j,k} = \Delta x^2 R_{j,k}. \qquad(12)\] Let the \((N+1)^2\) vector of unknowns be denoted by \(\vec{x}\), which contains \(u_{j,k}\) elements.

The matrix form of Equation 12 is \(\hat{A}\cdot\vec{X}=\vec{b}\)

1.28 Solution methods for elliptic PDEs

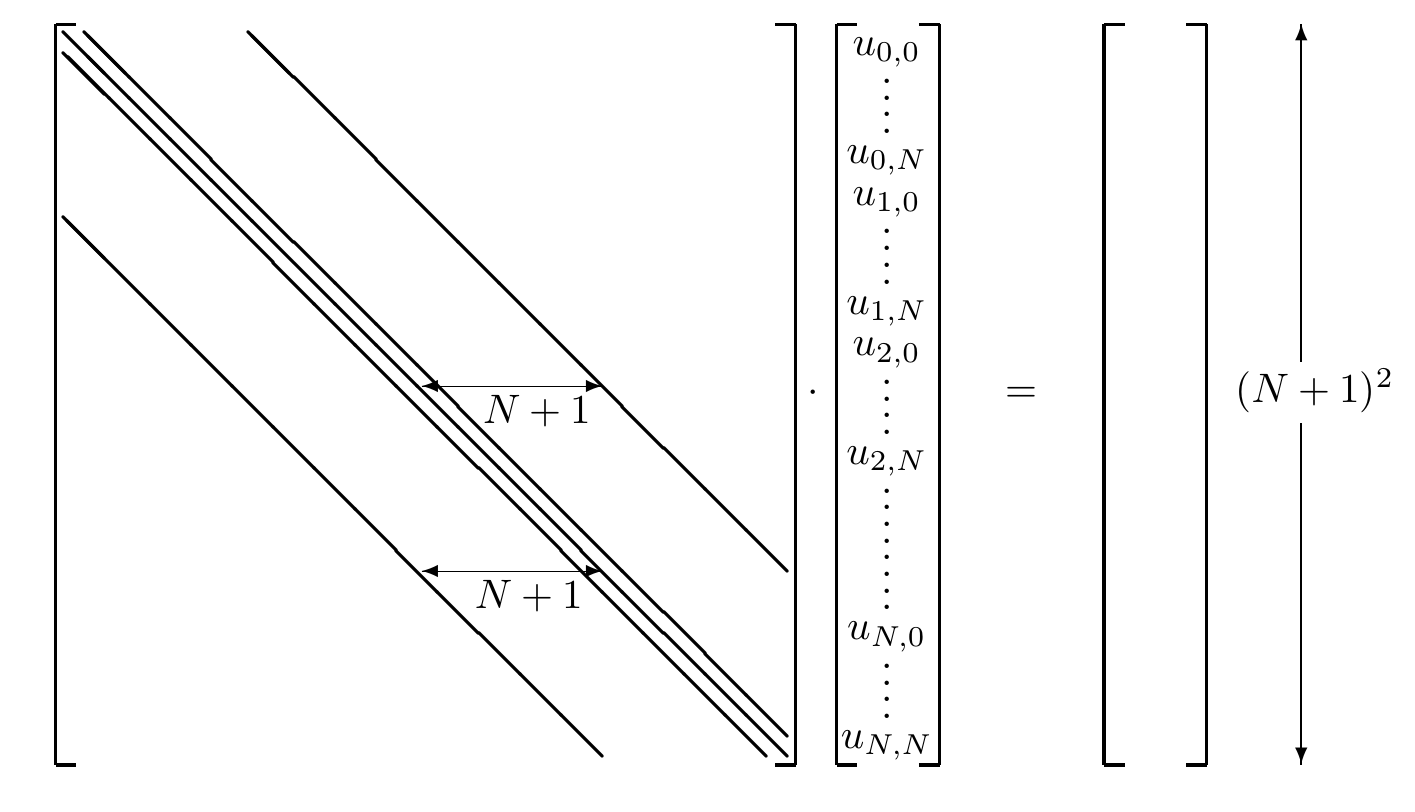
Sparse matrix \(\hat{A}\):

• Must be inverted to solve for the unknowns (although the actual inverse is not normally calculated). Some methods are:
  • Direct inversion using Gauss or LU decomposition
  • Direct inversion using block tri-diagonal methods
  • Iterative methods (multigrid, Krylov space methods). A physical approach involves adding time derivatives terms (converting it to parabolic/hyperbolic equations), and advancing it in time until a steady state is obtained.
  • Direct methods based on transform techniques (e.g., Fourier transformation)

1.29 Multigrid methods

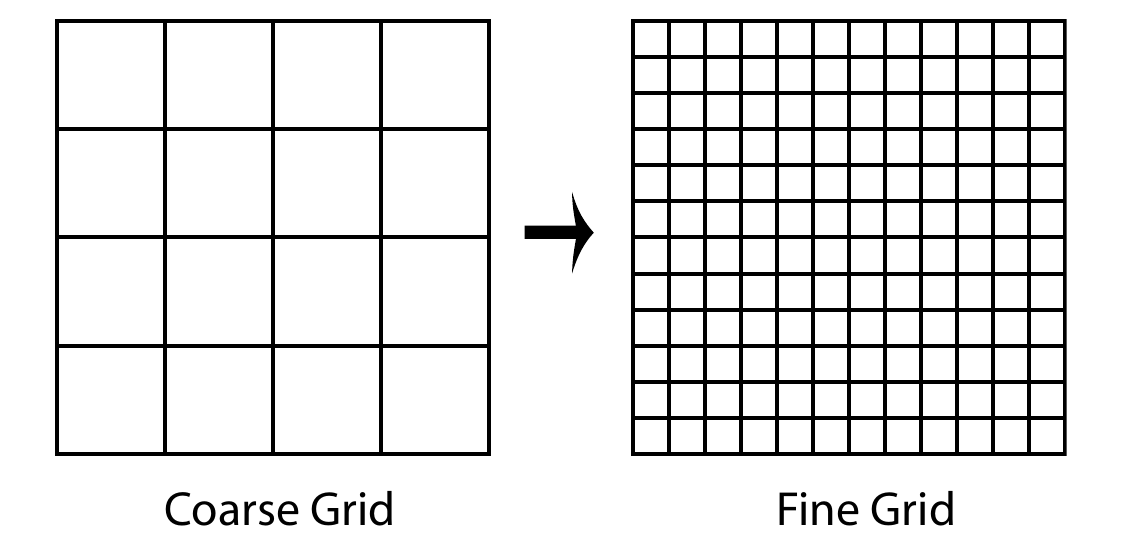
Schematics of multigrid method

• Iterative methods benefit greatly from a good initial guess: A coarse grid solution can be used to initialize a finer grid iteration
• On a given grid, the short wavelengths components of the error decay much faster than the long wavelengths. So, the coarse mesh is more efficient in handling long components of the error but the fine mesh is needed for the short wavelength components.
• The error satisfies the same matrix eqs. as the unknown.
• Two basic steps: nested iteration (for the initial guess), coarse grid correction.

1.30 Fast Fourier methods

• Fourier (spectral) methods can be applied to solve boundary problems (e.g., elliptic equations) that lead to large sparse linear systems of the form \(\hat{A}\cdot\vec{u}=\vec{b}\)
• The algorithm is based on a Fast Fourier transform (FFT), a clever trick to avoid the calculation of \(N^2\) multiplications and \(N(N-1)\) that are required for a direct finite Fourier transform. Instead, if \(N\) is equal to a power of 2, it leads to a product of \(log_2(N)\) sparse matrices.
• It works best when the PDE has constant coefficients and the boundaries coincide with the coordinate lines.

2 Introduction to testing particle method

2.1 Introduction

2.2 Hierarchy of plasma physics models

Kinetic description

Microscopic properties, it uses the velocity distribution function \(f\).

Fluid description

Uses a few macroscopic quantities, averages of the distribution function (mean velocity, pressure/temperature). Valid for or near thermodynamic equilibrium.

Hierarchy of plasma physics models

2.3 Motivation example (1/5)

Particles released during solar flare

2.4 Motivation example (2/5)

Particle motion around black holes

2.5 Motivation example (3/5)

Particles hitting space probes (Voyager)

2.6 Motivation example (3/5)

Particles hitting space probes (Voyager)

2.7 Motivation example (4/5)

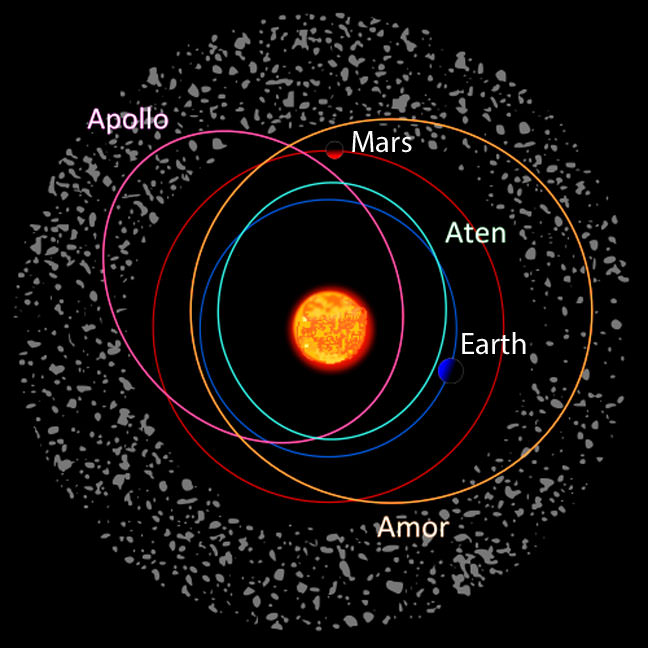
Asteroid motion in space system - potential threat on the Earth

2.8 Motivation example (5/5)

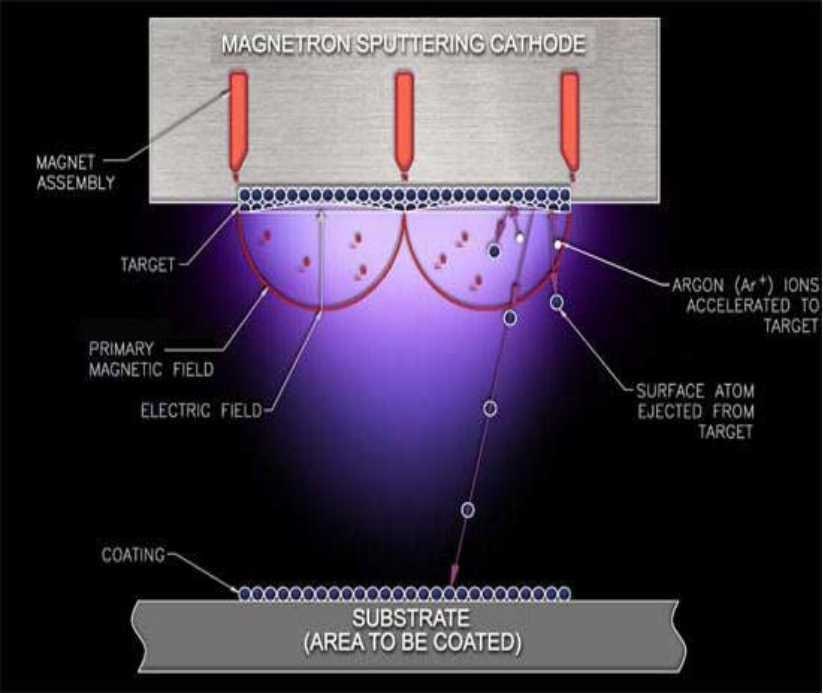
Magnetron coating

2.9 Distribution function and phase space

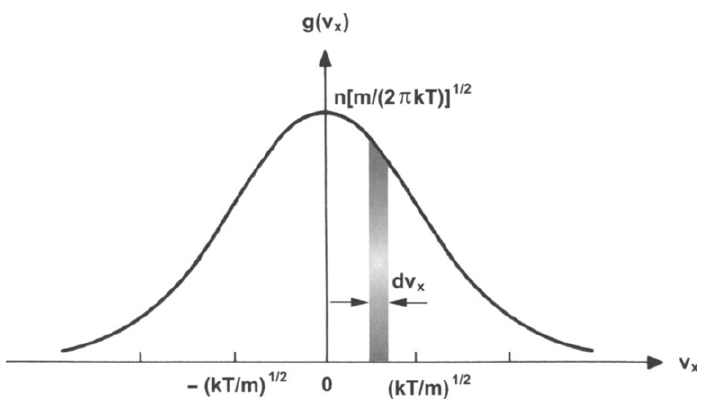
• Distribution function \(f(\vec{x},\vec{v},t)\)
• Probability density of finding any particle in the phase space volume element \([x,x+dx],[y,y+dy],[z,z+dz]\) and with velocities \([v_x,v_x+dv_x],[v_y,v_y+dv_y],[v_z,v_z+dv_z]\) such that: \[ d^6N = f(\vec{x},\vec{v},t)\cdot d^3\vec{x} \cdot d^3\vec{v} \]

2.10 Maxwell-Boltzmann distribution function

• The Maxwell-Boltzmann distribution represents the thermal equilibrium. It is a stationary and homogeneous solution of the kinetic equations. \[ f_{\alpha} (\vec{v},T_\alpha)=n_{0{\alpha}}\left(\frac{m_{\alpha}}{2\pi k_B T_{\alpha}}\right)^{3/2}\exp\left(-\frac{m_{\alpha}\vec{v}^2}{2k_BT_{\alpha}}\right) \]

2.11 Full equations of motion

Full equations of motion

\[ \nabla\cdot\vec{E}(\vec{x},t)=\frac{\rho(\vec{x},t)}{\epsilon_0}\\ \nabla\cdot\vec{B}(\vec{x},t)=0\\ \nabla\times\vec{E}(\vec{x},t)=-\frac{\partial \vec{B}(\vec{x},t)}{\partial t}\\ \nabla\times\vec{B}(\vec{x},t)=\mu_0\vec{J}(\vec{x},t)+\mu_0\epsilon_0\frac{\partial \vec{E}(\vec{x},t)}{\partial t} \]

\[ \frac{dv_i}{dt}=\frac{q}{m}\left[\vec{E}(\vec{x}_i,t) + \vec{v}\times\vec{B}(\vec{x}_i,t) \right] \]

\[ \rho(\vec{x},t)=\sum\limits_{\alpha} q_{\alpha}\int\limits dv^3\,\sum_i\delta(\vec{x}-\vec{x_i})\delta(\vec{v}-\vec{v_i})\\ \vec{J}(\vec{x},t)=\sum\limits_{\alpha} q_{\alpha}\int dv^3\,\vec{v}\sum_i\delta(\vec{x}-\vec{x_i})\delta(\vec{v}-\vec{v_i}) \]

But this approach is unpractical…

2.12 Physicists encountering a new field

Title text: If you need some help with the math, let me know, but that should be enough to get you started! Huh? No, I don’t need to read your thesis, I can imagine roughly what it says. https://xkcd.com/793/

2.13 Simplified set of equations

Simplified set

\[ \frac{dv_i}{dt}=\frac{q}{m}\left[\vec{E}(\vec{x}_i,t) + \vec{v}\times\vec{B}(\vec{x}_i,t) \right] \]

2.14 The test particle method

• Decouple Maxwell equations. Obtain electromagnetic fields \(\vec{E}\), \(\vec{B}\) (or other forces) from another methods or observations.
• Integrate particle trajectories using those electromagnetic fields via, e.g.,
  1. Full Lorentz force: \[ \frac{dv_i}{dt}=\frac{q}{m}\left[\vec{E}(\vec{x}_i,t) + \vec{v}\times\vec{B}(\vec{x}_i,t) \right] + \textrm{Other forces} \qquad(13)\]
  2. (Optional) Guiding center approximation.
  3. Repeat points 1 and 2 for each particle
  4. Use the particle trajectories to infer approximate kinetic properties of the system.
• Examples of other forces: Gravitational force, radiation force, particle collisitions, …

Warning

This approach is not self-consistent, the particles do not have any effect on the fields or other particles (no feedback or correction).

3 Integration of particle trajectories

3.1 Runge-Kutta methods

3.2 2nd-order Runge-Kutta

• It is based on the exact integration of \(\frac{dy}{dt}=f(t,y)\) \ in times \(t_0, t_1, \ldots t_{i}, t_{i+1}, \ldots\) \[ y_{t_{i+1}}=y_{t_{i}} + \int\limits_{t_{i}}^{t_{i+1}}f(t,y)dt \qquad(14)\]
• The basis for RK2 is to approximate \(f(t,y)\) by a Taylor expansion w/r to the time middle point \(t_{i+1/2} = t_i + \Delta t / 2\): \[ f(t,y)\approx f(t_{i+1/2},y_{i+1/2}) + (t- t_{i+1/2})\frac{df}{dt}\Bigg|_{t_{i+1/2}} \]
• Since the integral of the 2nd term vanishes, \[ y_{i+1}=y_i + \Delta t \cdot f(t_{i+1/2},y_{i+1/2}) + \mathcal{O}(\Delta t^3) \]
• Finally, the value of \(y_{i+1/2}\) is obtained by the Euler’s method: \(y_{i+1/2}\approx y_i+\frac{\Delta t}{2}f(t_i,y_i)\).

2nd-order Runge-Kutta (RK2)

\[ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f \left( t_i+\frac{\Delta t}{2},y_i+\frac{k_1}{2} \right) \\ y_{i+1}=y_i+k_2\\ \]

• The local/global error is \(\mathcal{O}(\Delta t^3)/\mathcal{O}(\Delta t^2)\).

3.3 Runge-Kutta methods: General derivation

• The family of Runge-Kutta methods are derived from the following Taylor expansion, without explicit calculation of the derivatives: \[ y(t_{i+1})=y(t_{i}+\Delta t)=y(t_i)+\Delta t \cdot y'(t_i)+\frac{\Delta t^2}{2}y''(t_i)+\cdots \]
• In particular, RK2 is obtained by finding the constants \(a_1,a_2,p_1,q_{11}\) such that the following formula coincides with the Taylor expansion to 2nd order: \[ y_{i+1}=y_i+a_1k_1+a_2k_2,\\ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f(t_i+ p_1 h,y_i + q_{11} k_1h) \]
• The solution is: \[ a_1+a_2=1,\qquad a_2p_1=\frac{1}{2},\qquad a_2q_{11}=\frac{1}{2} \]
• Since there are 3 eqs but 4 unknowns, there is some freedom of choice. By choosing \(a_2=1/2\), we get the (improved) Euler’s method. Choosing \(a_2=1\), we get RK2 with \(a_1=0\), \(p_1=1/2\), \(q_{11}=1/2\).

3.4 4th-order Runge Kutta

• By considering more terms in the Taylor expansion, it is possible to improve the precision of RK2. The most popular algorithm (since \(\sim\) 1900) is:

4th-order Runge Kutta (classic RK, RK4)

\[ y_{i+1}=y_i+\frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)\\ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f(t_i+\frac{\Delta t}{2},y_i+\frac{k_1}{2})\\ k_3=\Delta t \cdot f(t_i+\frac{\Delta t}{2},y_i+\frac{k_2}{2})\\ k_4=\Delta t \cdot f(t_i+\Delta t,y_i+k_3) \]

• Global/local error \(\mathcal{O}(\Delta t^5)\)/\(\mathcal{O}(\Delta t^4)\)
• RK4 estimates the value of \(y_{i+1}\) by averaging 4 slopes
• It provides a good balance between accuracy and computational cost

3.5 4th-order Runge Kutta

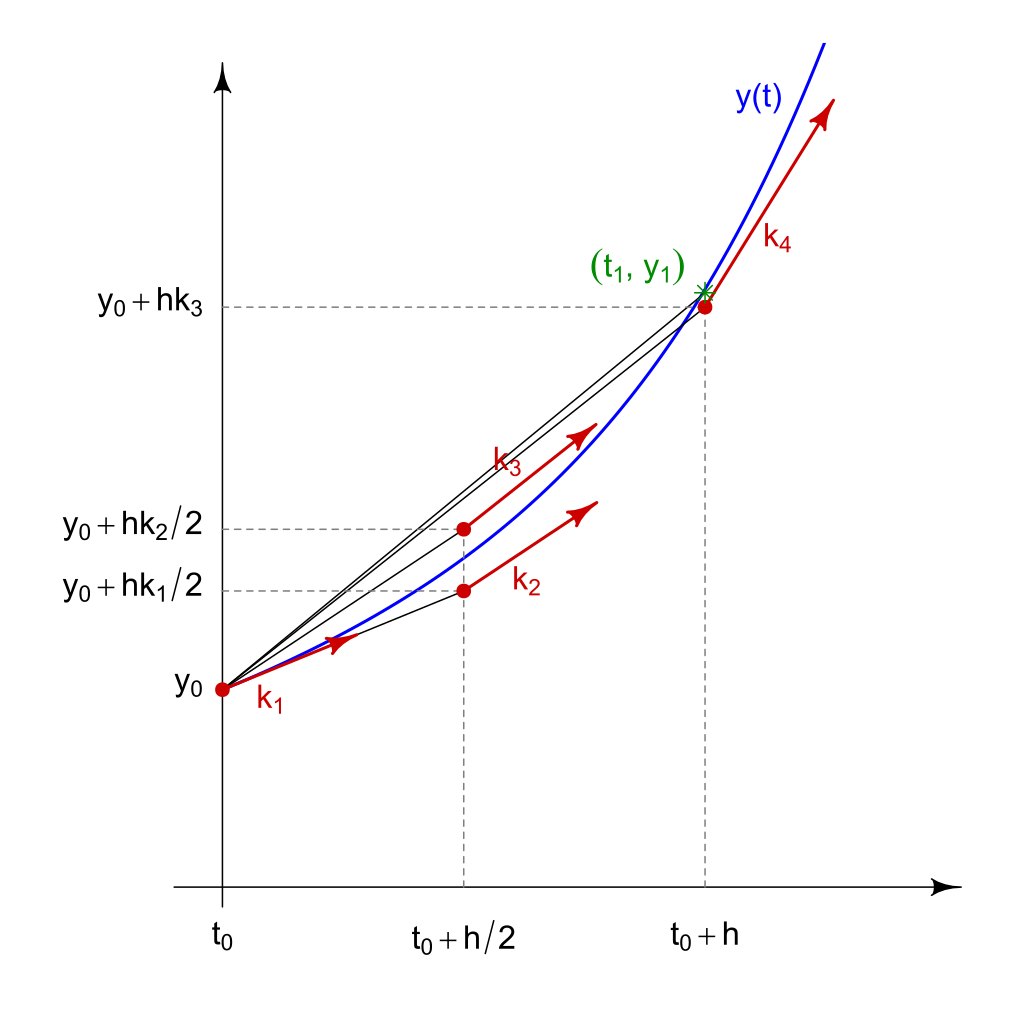
Slopes used for the Runge-Kutta method; \(h = \Delta t\)

3.6 4th-order Runge Kutta

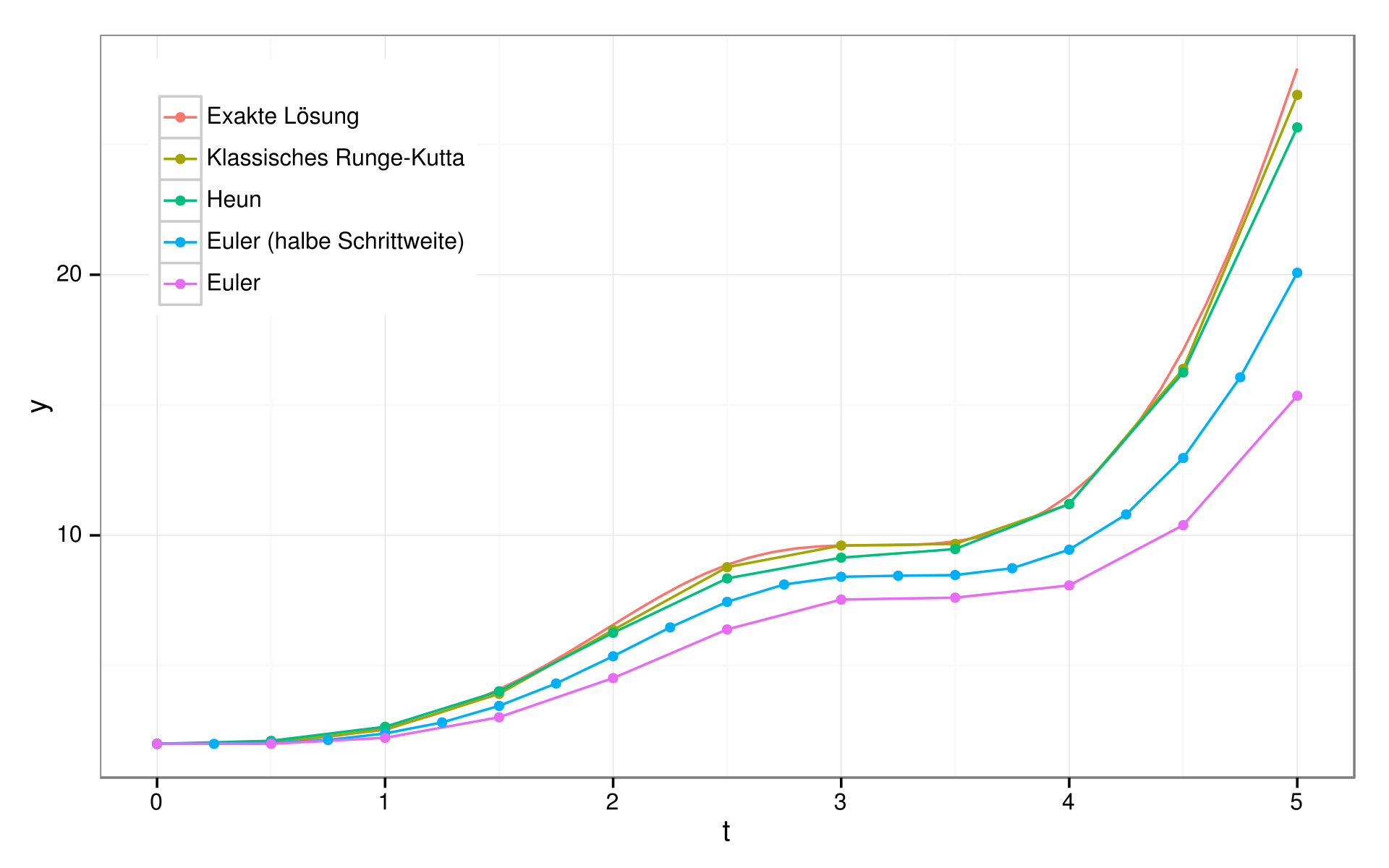
Comparison of Runge-Kutta with other methods for the solution of the ODE: \(y'=sin^2(t)*y\)

3.7 Symplectic methods

3.8 Symplectic methods

• When we apply conventional methods like Euler’s or RK to a Hamiltonian system, an artificial excitation or damping occurs.
• Hamiltonian energy \[ H(q,p,t) = T + V \] with canonical coordinates \(q,p\)
• For autonomous Hamiltonian systems: \[ \frac{dq}{dt}=\frac{\partial H}{\partial p},\;\; \frac{dp}{dt}=-\frac{\partial H}{\partial q} \] \(H\) is conserved and the two-form \(dp\wedge dq\) = constant (Jacobian)
• A numerical integration scheme satisfying those two properties is symplectic, they preserve the phase space density. They conserve the energy (time-reversible).

3.9 Symplectic methods

• Assuming known the Hamiltonian (\(\sim\) energy) of the system, symplectic methods can be written as an n-iteration of: \[ x_{i}=x_{i-1}+c_i\Delta t\, v_{i-1}\\ v_{i}=v_{i-1}+d_i\Delta t\, a(x_i) \qquad(15)\] where \(a=F/m\) and \(c_i\), \(d_i\) are constants.
• There are explicit symplectic algorithms for separable Hamiltonians: \(H=T(p) + V(q)\) (conservative systems). Note that unfortunately the Hamiltonian of charged particles in EM fields is not separable: \(H(\vec{p},\vec{x})=(1/2)(\vec{p}-\vec{A})^2 + \phi\).
• More info: Yoshida (1993)

3.10 Verlet’s algorithm

• Example for the 2nd Newton’s law: using a finite central difference of 2nd order for \(\frac{d^2x}{dt^2} = F/m = a\), and central difference for the first derivative \(\frac{dx}{dt} = v\).
• We get an algorithm very useful for N-body problems (Verlet used it for molecular dynamics), which is also symplectic: \(c_1=c_2=1/2\), \(d_1=1\), \(d_2=0\).

Verlet’s (Störmer) algorithm

\[ \vec{x}_{i+1}=2\vec{x}_i-\vec{x}_{i-1}+(\Delta t)^2\vec{a}_i+\mathcal{O}(\Delta t)^4\\ \vec{v}_i=\frac{\vec{x}_{i+1}-\vec{x}_{i-1}}{2\Delta t}+\mathcal{O}(\Delta t)^2 \]

• The local/global error is \(\mathcal{O}(h^4)/\mathcal{O}(h^2)\).
• Initialization: multistep method: 2 initial positions are required: \(\vec{x}_{0}\) and \(\vec{x}_{1}\).
• Usually we know only the initial conditions \(\vec{x}_{0}\) and \(\vec{v}_{0}\). We can assume \(\vec{F}=constant\) in the first interval \([0,\Delta t]\), so that we can use \(\vec{x}_1\approx\vec{x}_0 + \Delta t \vec{v}_0+\vec{a}_0 \frac{\Delta t^2}{2}\)

3.11 Examples of usage of Verlet’s algorithm

• Störmer problem: to determine the orbits of charged particles in the Earth’s magnetic field. Originally (1907) aimed at understanding the aurora.
• Molecular dynamics
• Computer games

3.12 Boris algorithm

• Specifically used to advance particles in plasma simulations (it is the de facto algorithm).
• It has very good conservation properties: it conserves phase space volume, even though it is not symplectic (Qin et al. (2013)):
• Discretized Lorentz force: \[ \frac{\vec{x}_{i+1} - \vec{x}_i}{\Delta t} = v_{i+1} \\ \frac{\vec{v}_{i+1} - \vec{v}_i}{\Delta t} = \frac{q}{m}\left(\vec{E}_i +(\vec{v}_{i+1} - \vec{v}_i)\times\vec{B}_i \right) \]
• The idea of the Boris algorithm is to separate the electric and magnetic force in 3 parts: first half of the electric force is determined, then the full magnetic force (rotation) and finally the second half of the electric force.

3.13 Boris algorithm

Comparison of energies of a charged particle moving in a given B-field, with its trajectory calculated using the RK4 and Boris algorithms (Qin et al. (2013))

3.14 References

Jardin, S. 2010. Computational Methods in Plasma Physics. CRC Press.

Press, William H., Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. 2007. Numerical Recipes: The Art of Scientific Computing. Third Edition. Cambridge University Press. https://doi.org/10.1137/1031025.

Qin, Hong, Shuangxi Zhang, Jianyuan Xiao, Jian Liu, Yajuan Sun, and William M Tang. 2013. “Why is Boris algorithm so good?” Phys. Plasmas 20 (8): 084503. https://doi.org/10.1063/1.4818428.

Yoshida, Haruo. 1993. “Recent Progress in the Theory and Application of Symplectic Integrators.” Celest. Mech. Dyn. Astron. 56: 27–43. https://doi.org/10.1007/978-94-011-2030-2_3.