Lecture 4: Test particles – lecture + hands-on

Jan Benáček

Institute for Physics and Astronomy, University of Potsdam

November 14, 2024

Lecture overview

Table of Contents 1/2

  • 17.10. Introduction + numerical methods summary
  • 24.10. Numerical methods of differential equations — lecture + hands-on
  • 31.10. State holiday
  • 07.11. Test particle approach — lecture
  • 14.11. Test particle approach — lecture + hands-on
  • 21.11. PIC method — lecture
  • 28.11. PIC method — hands-on

Table of Contents 2/2

  • 05.12. Fluid and MHD — lecture
  • 12.12. Canceled
  • 19.12. Fluid and MHD — hands-on
  • 09.01. Radiative transfer — lecture + hands-on
  • 16.01. HPC computing — lecture + hands-on
  • 23.01. Advanced — Smooth particle hydrodynamics method — lecture
  • 30.01. Advanced — Hybrid, Gyrokinetics — lecture
  • 06.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture

1 Integration of particle trajectories

1.1 Runge-Kutta methods

1.2 2nd-order Runge-Kutta

  • It is based on the exact integration of \(\frac{dy}{dt}=f(t,y)\) \ in times \(t_0, t_1, \ldots t_{i}, t_{i+1}, \ldots\) \[ y_{t_{i+1}}=y_{t_{i}} + \int\limits_{t_{i}}^{t_{i+1}}f(t,y)dt \qquad(1)\]
  • The basis for RK2 is to approximate \(f(t,y)\) by a Taylor expansion w/r to the time middle point \(t_{i+1/2} = t_i + \Delta t / 2\): \[ f(t,y)\approx f(t_{i+1/2},y_{i+1/2}) + (t- t_{i+1/2})\frac{df}{dt}\Bigg|_{t_{i+1/2}} \]
  • Since the integral of the 2nd term vanishes, \[ y_{i+1}=y_i + \Delta t \cdot f(t_{i+1/2},y_{i+1/2}) + \mathcal{O}(\Delta t^3) \]
  • Finally, the value of \(y_{i+1/2}\) is obtained by the Euler’s method: \(y_{i+1/2}\approx y_i+\frac{\Delta t}{2}f(t_i,y_i)\).

2nd-order Runge-Kutta (RK2)

\[ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f \left( t_i+\frac{\Delta t}{2},y_i+\frac{k_1}{2} \right) \\ y_{i+1}=y_i+k_2\\ \]

  • The local/global error is \(\mathcal{O}(\Delta t^3)/\mathcal{O}(\Delta t^2)\).

1.3 Runge-Kutta methods: General derivation

  • The family of Runge-Kutta methods are derived from the following Taylor expansion, without explicit calculation of the derivatives: \[ y(t_{i+1})=y(t_{i}+\Delta t)=y(t_i)+\Delta t \cdot y'(t_i)+\frac{\Delta t^2}{2}y''(t_i)+\cdots \]
  • In particular, RK2 is obtained by finding the constants \(a_1,a_2,p_1,q_{11}\) such that the following formula coincides with the Taylor expansion to 2nd order: \[ y_{i+1}=y_i+a_1k_1+a_2k_2,\\ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f(t_i+ p_1 h,y_i + q_{11} k_1h) \]
  • The solution is: \[ a_1+a_2=1,\qquad a_2p_1=\frac{1}{2},\qquad a_2q_{11}=\frac{1}{2} \]
  • Since there are 3 eqs but 4 unknowns, there is some freedom of choice. By choosing \(a_2=1/2\), we get the (improved) Euler’s method. Choosing \(a_2=1\), we get RK2 with \(a_1=0\), \(p_1=1/2\), \(q_{11}=1/2\).

1.4 4th-order Runge Kutta

  • By considering more terms in the Taylor expansion, it is possible to improve the precision of RK2. The most popular algorithm (since \(\sim\) 1900) is:

4th-order Runge Kutta (classic RK, RK4)

\[ y_{i+1}=y_i+\frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)\\ k_1=\Delta t \cdot f(t_i,y_i)\\ k_2=\Delta t \cdot f(t_i+\frac{\Delta t}{2},y_i+\frac{k_1}{2})\\ k_3=\Delta t \cdot f(t_i+\frac{\Delta t}{2},y_i+\frac{k_2}{2})\\ k_4=\Delta t \cdot f(t_i+\Delta t,y_i+k_3) \]

  • Global/local error \(\mathcal{O}(\Delta t^5)\)/\(\mathcal{O}(\Delta t^4)\)
  • RK4 estimates the value of \(y_{i+1}\) by averaging 4 slopes
  • It provides a good balance between accuracy and computational cost

1.5 4th-order Runge Kutta

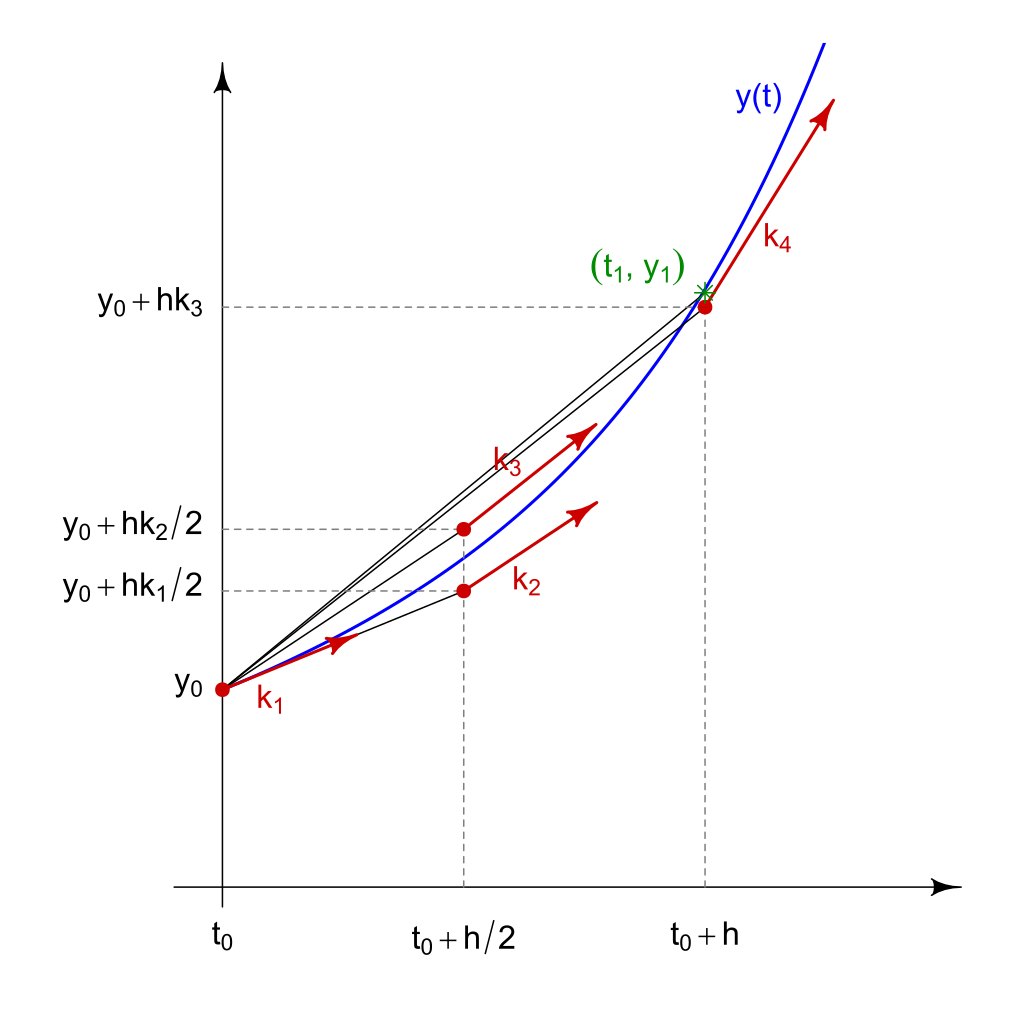
Slopes used for the Runge-Kutta method; \(h = \Delta t\)

1.6 4th-order Runge Kutta

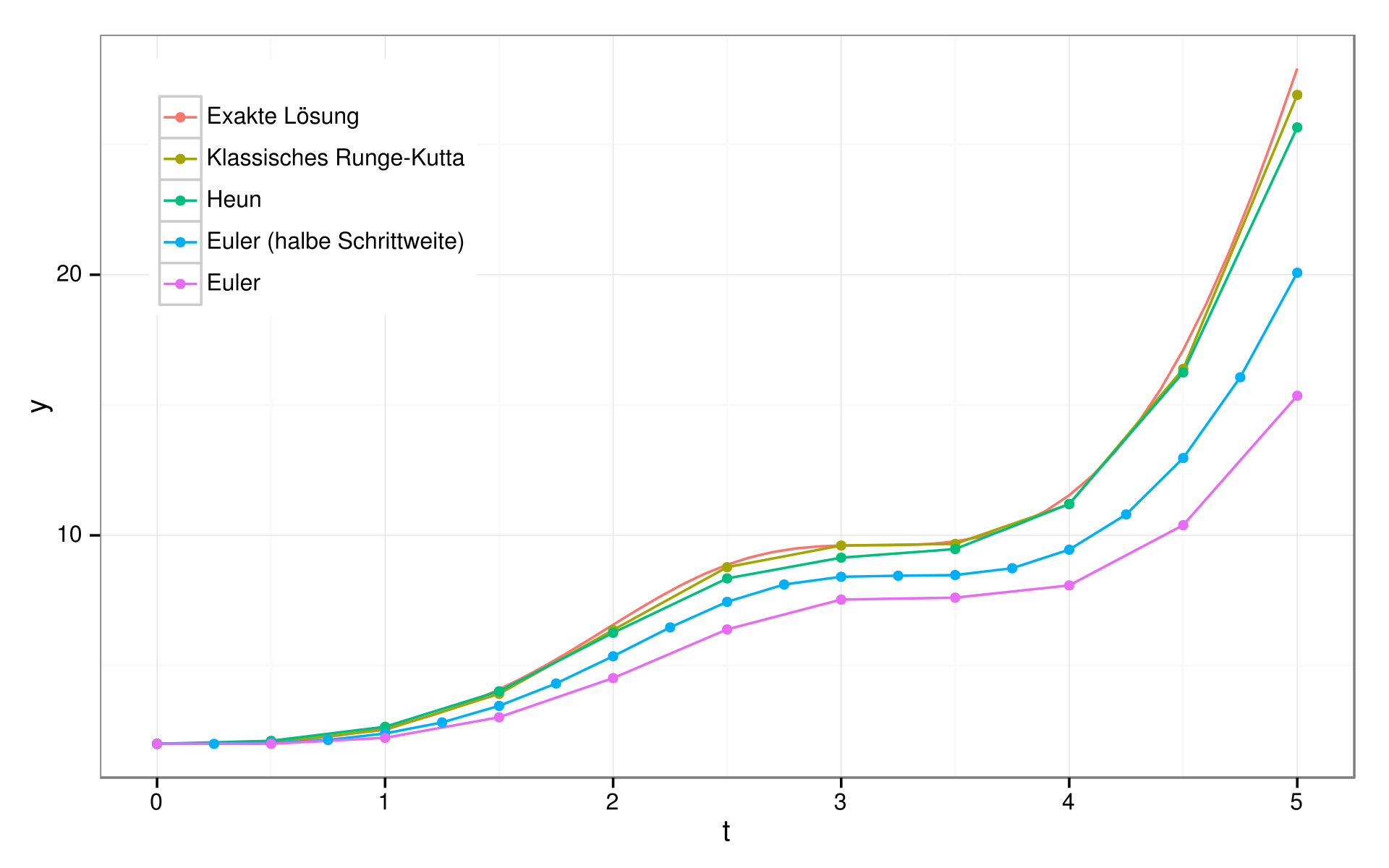
Comparison of Runge-Kutta with other methods for the solution of the ODE: \(y'=sin^2(t)*y\)

1.7 Symplectic methods

1.8 Symplectic methods

  • When we apply conventional methods like Euler’s or RK to a Hamiltonian system, an artificial excitation or damping occurs.
  • Hamiltonian energy \[ H(q,p,t) = T + V \] with canonical coordinates \(q,p\)
  • For autonomous Hamiltonian systems: \[ \frac{dq}{dt}=\frac{\partial H}{\partial p},\;\; \frac{dp}{dt}=-\frac{\partial H}{\partial q} \] \(H\) is conserved and the two-form \(dp\wedge dq\) = constant (Jacobian)
  • A numerical integration scheme satisfying those two properties is symplectic, they preserve the phase space density. They conserve the energy (time-reversible).

1.9 Symplectic methods

  • Assuming known the Hamiltonian (\(\sim\) energy) of the system, symplectic methods can be written as an n-iteration of: \[ x_{i}=x_{i-1}+c_i\Delta t\, v_{i-1}\\ v_{i}=v_{i-1}+d_i\Delta t\, a(x_i) \qquad(2)\] where \(a=F/m\) and \(c_i\), \(d_i\) are constants.
  • There are explicit symplectic algorithms for separable Hamiltonians: \(H=T(p) + V(q)\) (conservative systems). Note that unfortunately the Hamiltonian of charged particles in EM fields is not separable: \(H(\vec{p},\vec{x})=(1/2)(\vec{p}-\vec{A})^2 + \phi\).
  • More info: Yoshida (1993)

1.10 Verlet’s algorithm

  • Example for the 2nd Newton’s law: using a finite central difference of 2nd order for \(\frac{d^2x}{dt^2} = F/m = a\), and central difference for the first derivative \(\frac{dx}{dt} = v\).
  • We get an algorithm very useful for N-body problems (Verlet used it for molecular dynamics), which is also symplectic: \(c_1=c_2=1/2\), \(d_1=1\), \(d_2=0\).

Verlet’s (Störmer) algorithm

\[ \vec{x}_{i+1}=2\vec{x}_i-\vec{x}_{i-1}+(\Delta t)^2\vec{a}_i+\mathcal{O}(\Delta t)^4\\ \vec{v}_i=\frac{\vec{x}_{i+1}-\vec{x}_{i-1}}{2\Delta t}+\mathcal{O}(\Delta t)^2 \]

  • The local/global error is \(\mathcal{O}(h^4)/\mathcal{O}(h^2)\).
  • Initialization: multistep method: 2 initial positions are required: \(\vec{x}_{0}\) and \(\vec{x}_{1}\).
  • Usually we know only the initial conditions \(\vec{x}_{0}\) and \(\vec{v}_{0}\). We can assume \(\vec{F}=constant\) in the first interval \([0,\Delta t]\), so that we can use \(\vec{x}_1\approx\vec{x}_0 + \Delta t \vec{v}_0+\vec{a}_0 \frac{\Delta t^2}{2}\)

1.11 Examples of usage of Verlet’s algorithm

  • Störmer problem: to determine the orbits of charged particles in the Earth’s magnetic field. Originally (1907) aimed at understanding the aurora.
  • Molecular dynamics
  • Computer games

1.12 Boris algorithm

  • Specifically used to advance particles in plasma simulations (it is the de facto algorithm).
  • It has very good conservation properties: it conserves phase space volume, even though it is not symplectic (Qin et al. (2013)):
  • Discretized Lorentz force: \[ \frac{\vec{x}_{i+1} - \vec{x}_i}{\Delta t} = v_{i+1} \\ \frac{\vec{v}_{i+1} - \vec{v}_i}{\Delta t} = \frac{q}{m}\left(\vec{E}_i +(\vec{v}_{i+1} - \vec{v}_i)\times\vec{B}_i \right) \]
  • The idea of the Boris algorithm is to separate the electric and magnetic force in 3 parts: first half of the electric force is determined, then the full magnetic force (rotation) and finally the second half of the electric force.

1.13 Boris algorithm

Comparison of energies of a charged particle moving in a given B-field, with its trajectory calculated using the RK4 and Boris algorithms (Qin et al. (2013))

2 Particle drifts/guiding center

2.1 Particle drifts

2.2 Particle motion in background magnetic fields

  • The basic motion of a particle under the influence of a static and uniform magnetic field is the gyromotion.
  • Taking the dot product of Equation (13) from the last lecture with \(\vec{v}\), we get \[ \frac{d}{dt}\left(\frac{mv^2}{2}\right) = 0. \] That is, a static magnetic field cannot change the kinetic energy of a particle.

2.3 Particle motion in background magnetic fields

  • Assuming a magnetic field \(\vec{B}=B\hat{z}\), the equation becomes: \[ m\frac{dv_x}{dt}=qB v_y\\ m\frac{dv_y}{dt}=-qB v_x\\ m\frac{dv_z}{dt}=0 \] and thus, \[ \frac{d^2v_x}{dt^2} + \Omega_c^2 v_x=0\\ \frac{d^2v_y}{dt^2} + \Omega_c^2 v_y=0 \]

2.4 Particle motion in background magnetic fields

  • Where the gyrofrequency (or Larmor/cyclotron) is: \[ \Omega_c=\frac{qB}{m} \]
  • Solution \[ v_x = v_{\perp}\cos\left( \Omega_c t + \psi \right) \\ v_y = v_{\perp}\sin\left( \Omega_c t + \psi \right) \\ v_z=v_{\parallel} \] where \(\psi\) is an arbitrary phase angle.
  • By integrating we get, \[ x = \rho_c\sin\left( \Omega_c t + \psi \right) + (x_0 - r_c\sin\psi) \\ y = -\rho_c\cos\left( \Omega_c t + \psi \right) + (y_0 + r_c\cos\psi) \\ z=z_0 + v_{\parallel}t \qquad(3)\]

2.5 Particle motion in background magnetic fields

  • Where the gyroradius (or Larmor radius or cyclotron radius) is: \[ \rho_c=\frac{|v_{\perp}|}{\Omega_c}=\frac{m|v_{\perp}|}{|q|B} \] Note that this can be understood from force balancing the “centrifugal” force: \[ \frac{mv_{\perp}^2}{r}=qv_{\perp}B \]
  • Particles move in circular/helical orbits with frequency \(\Omega_c\) and radius \(\rho_c\) about the guiding center \[ R_g=\hat{x}x_0 + \hat{y}y_0 + \hat{z}(z_0 + v_{\parallel}t) \]
  • Note that particles with higher velocities orbit in circles with larger radii, but the same frequency.
  • Particles with larger masses orbit in circles with larger radii, but with lower frequencies (longer periods).

2.6 Particle motion in magnetic fields (helical motion)

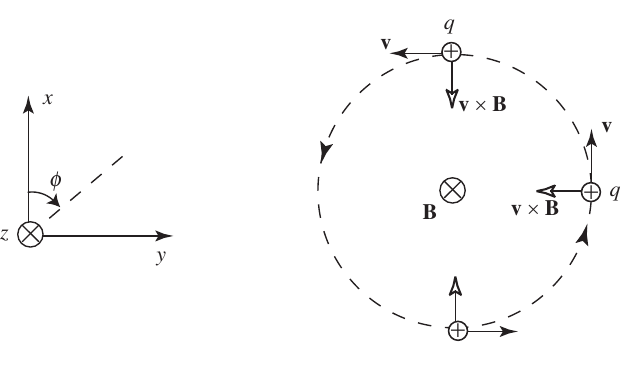
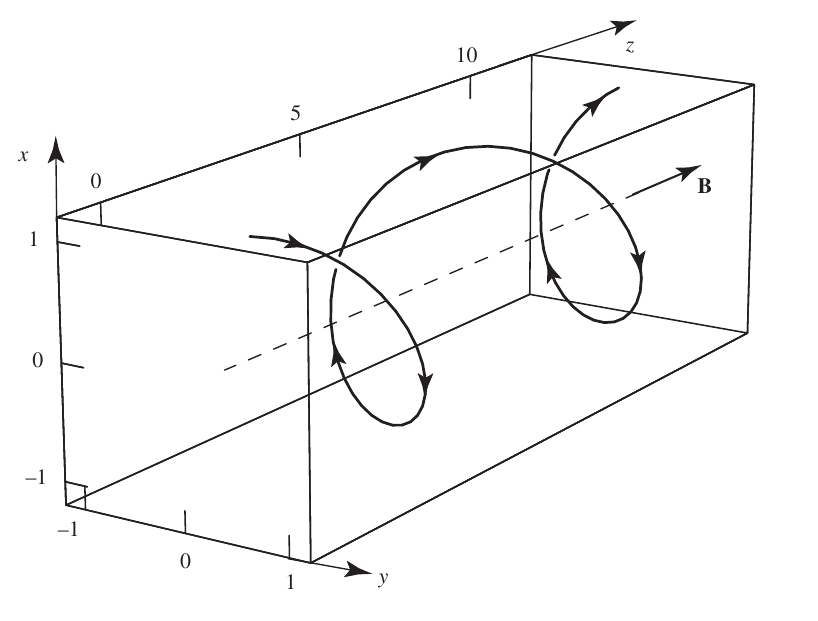
2.7 Particle motion in background magnetic fields

  • Pitch angle: \[ \alpha=\tan^{-1}\left(\frac{v_{\perp}}{v_{\parallel}}\right) \]
  • Magnetic moment \[ \mu=\underbrace{\frac{q\Omega_c}{2\pi}}_{\text{current}}\underbrace{\pi \rho_c^2}_{\text{area}}=\frac{mv_{\perp}^2}{2B} \]
  • The direction of the magnetic field generated by the gyration is opposite to that of the external field: a plasma is a diamagnetic medium.

2.8 \(\vec{E}\times\vec{B}\) drift

  • Let us consider, in addition to \(\vec{B}=\hat{z}B\), an electric field:
    \(\vec{E}=\hat{x}E_{\perp} + \hat{z}E_{\parallel}\). The equations of motions are: \[ \label{ecross1} m\frac{d\vec{v}_{\perp}}{dt}=q(\hat{x}E_{\perp} + \vec{v}_{\perp}\times \hat{z}B)\\ m\frac{dv_{\parallel}}{dt}=qE_{\parallel} \qquad(4)\]
  • Let us decompose \(\vec{v}_{\perp}=\vec{v}_E + \vec{v}_{ac}\). By choosing: \[ \vec{v}_E=\frac{\vec{E}\times\vec{B}}{B^2} \]
  • Equation 4 becomes the eq. for gyration with frequency \(\Omega_c\). \[ m\frac{d\vec{v}_{ac}}{dt}=q\vec{v}_{ac}\times\hat{z}B \]
  • The solution is then: \[ \vec{v}(t)=\hat{z} v_{\parallel}(t) + \vec{v}_E + \vec{v}_{ac}(t) \]

2.9 \(\vec{E}\times\vec{B}\) drift

  • The average of \(\vec{v}\) over one gyroperiod is: \[ \langle \vec{v} \rangle = \hat{z} v_{\parallel} + \vec{v}_E \] so \(\vec{v}_E\) is the average perpendicular velocity.
  • This drift arises from the difference in the local gyroradius between top/bottom.
  • The \(\vec{E}\times\vec{B}\) drift is independent on \(q\), \(m\) and \(v_{\perp}\).

2.10 Gradient B drift

  • Let us assume a magnetic field with intensity varying in the perpendicular direction to the B-vector \(\vec{B}(y)=\hat{z}B_z(y)\).
  • This drift also arises from a force perpendicular to the magnetic field. Generalizing the expression for the \(\vec{E}\times\vec{B}\) force: \[ \vec{v}_F=\frac{\left( \frac{\vec{F}_{\perp}}{q} \right) \times\vec{B}}{B^2} \]

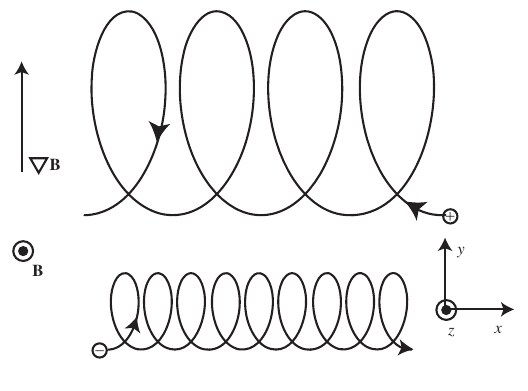
2.11 Gradient |B| drift

  • In this geometry, the perpendicular force is \[ \vec{F} = q\vec{v}\times\vec{B}=\hat{x}qv_yB_z - \hat{y}qv_xB_z \approx \hat{x}qv_y\left(B_0 + y\frac{\partial B_z}{\partial y} \right)-\hat{y}qv_x\left(B_0 + y\frac{\partial B_z}{\partial y} \right) \]
  • By assuming that particles follow approximately orbits in an uniform field (Equation 3), we can determine the gyroaverage force \(\vec{F}\): \[ \langle F_y \rangle = \frac{q v_{\perp} r_c}{2}\frac{\partial B_z}{\partial y}=\frac{m v_{\perp}^2}{2B}\frac{\partial B_z}{\partial y}\hspace{0.5cm}\text{or more generally}\hspace{0.5cm}=\frac{W_{\perp}}{B}\nabla |\vec{B}| \]
  • This way, the grad-B (\(\nabla \vec{B}\)) drift velocity is: \[ \vec{v}_{\nabla B} = \frac{ \vec{F}_{\perp} \times\vec{B}}{qB^2}=\frac{\langle\vec{F_y}\rangle\hat{y}\times\hat{z}B_z}{qB_z^2} = \frac{mv_{\perp}^2}{2qB_z}\frac{\partial B_z}{\partial y}\hat{x} \] or more generally \[ \vec{v}_{\nabla B} = \frac{mv_{\perp}^2}{2q}\frac{\vec{B}\times\nabla B}{B^3} \]

2.12 Curvature B drift

  • In a curved magnetic field line, particles experience a centrifugal force perpendicular to the B-field \[ \vec{F}_{cf}=mv_{\parallel}^2\frac{\vec{R}_c}{R_c^2} \] which causes a drift perpendicular to both vectors.

2.13 Curvature B drift

  • Curvature drift: \[ \vec{v}_{R} = \frac{ \left( \frac{\vec{F}_{cf}}{q} \right) \times\vec{B}}{B^2}= \frac{mv_{\parallel}^2}{q}\frac{\vec{R}_c\times\vec{B}}{R_c^2 B^2} \]
  • In vacuo this drift cannot be the only one because \(\nabla\times \vec{B} = 0\). A more general expression due to both gradient and curvature drifts is: \[ \vec{v}_{total}=\vec{v}_{R} + \vec{v}_{\nabla} =\left(v_{\parallel}^2 + \frac{v_{\perp}^2}{2} \right)\frac{\vec{B}\times\nabla B}{\Omega_c B^2} \]

2.14 Curvature B drift

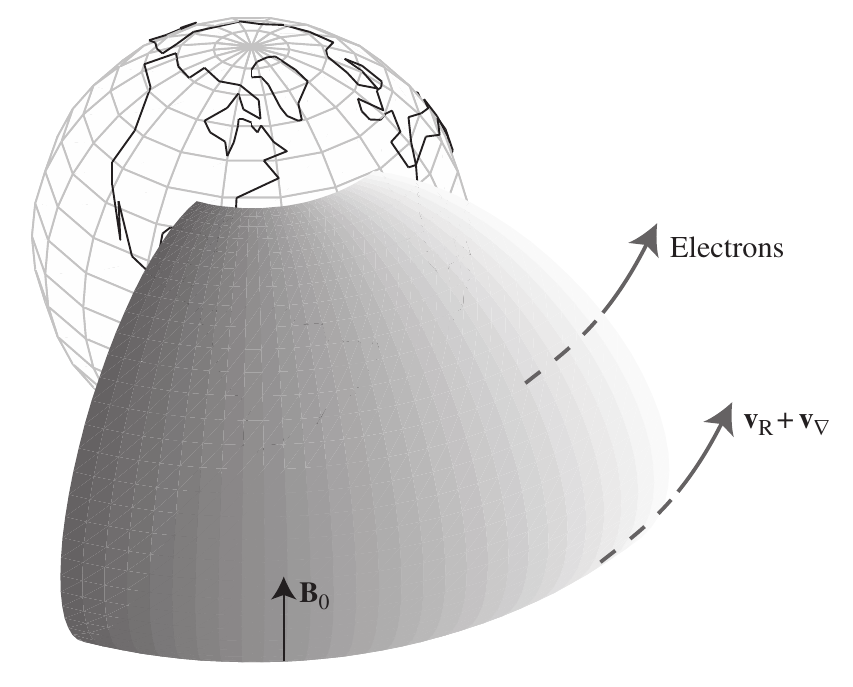
  • Longitudinal drift of radiation belt electrons (and associated ring current because of opposite ion/electron drift)

2.15 Adiabatic invariance of the magnetic moment

  • Magnetic moment \(\mu=\frac{mv_{\perp}^2}{2B}\) tends to be conserved as long as (spatial or temporal) changes in B are small over a gyroradius or gyroperiod.
  • The particle’s perpendicular energy increases while its parallel energy decreases as it moves toward regions of stronger B, until it eventually \(v_{\parallel}=0\) and it bounces back (magnetic mirror/bottle).

2.16 Particle trajectories in the Earth’s magnetosphere

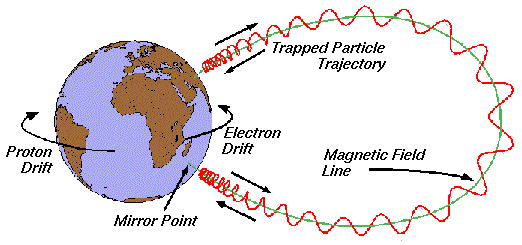
Credits: Spenvis (ESA’s SPace ENVironment Information System) Models description

2.17 Particle guiding center appoach

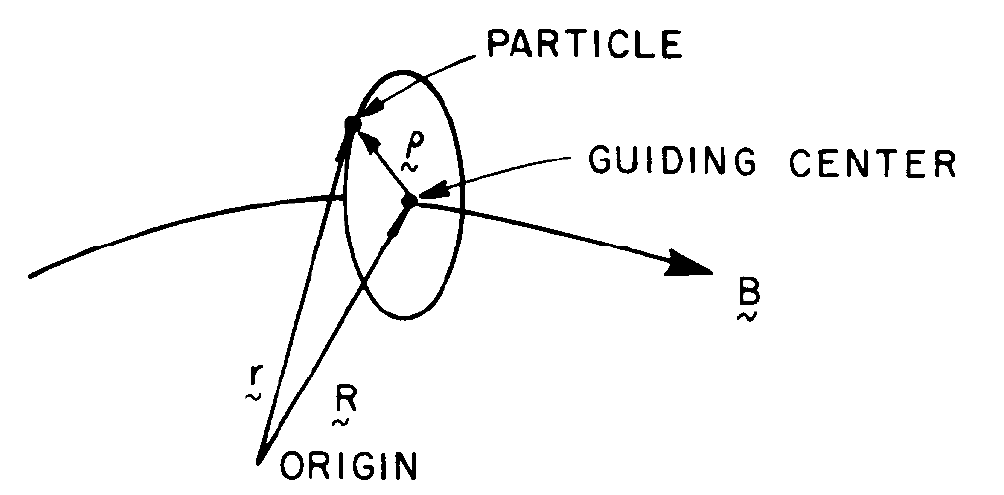
2.18 Guiding center approximation

  • Valid when the gyroradius (\(\rho= \frac{mv}{qB}\)) and gyroperiod (\(\propto \frac{1}{\Omega} = \frac{m}{qB}\)) are much smaller than the length scale of transverse gradients and characteristic oscillation periods of the background EM fields.

  • The motion of a charged particle is described in terms of variables representing the gyration around B-field lines and the motion of its guiding center.

  • For the solar corona, typical gyroradii are \(10^{-3} m\) for electrons and \(10^{-2} m\) for protons, much smaller than typical characteristic lengths scales.

3 Test particle algorithms

3.1 Test particle algorithms

3.2 Method 1: trajectory sampling

  • It solves individual representative trajectories (the choice is not trivial)
  • Useful to visualize aspects such as particle transport or energetics

3.3 Method 2: Forward Monte Carlo

  • Inject (randomly) particles in source regions where \(f\) is known, and follow them until they reach the regions of interest. Injected particles are tagged with a statistical weight \(w_i\) based on the number of injected particles per time \(\Gamma_{MC}\) and the physical flux \(\Gamma_{Phys}\): \[ w_i=\frac{\Gamma_{Phys}}{\Gamma_{MC}} \]
  • Statistical analysis of particles via sampling (binning) in \(x\) and \(v\) space (which implies large statistical errors), and using \(w_i\). For instance: \[ n=\frac{1}{\Delta x^3}\sum_i^N w_i \\ \Gamma_x=\frac{1}{\Delta x^3}\sum_i^N v_{ix}w_i \\ f(\vec{x},\vec{v})=\frac{1}{\Delta x^3\Delta v^3}\sum_i^N w_i \]
  • It is the most similar approach to the PIC method, but in this case with not self-consistent fields.

4 Hands-on

4.1 MHD simulation of magnetic reconnection (plasmoid/long current sheet)

4.2 Simple python code

  1. Read electromagnetic field data from MHD simulation snapshot (grid: 12802x 3202)
  2. Compute supplementary fields (like current density)
  3. Calculate electromagnetic fields at particles’ position (interpolation)
  4. Integrate particles using Lorentz force (or guiding center approximation) eq via Runge-Kutta 4th order (TODO: Boris pusher)
  5. Diagnostics (plots)
  • Normalizations, \(t_0 = 1s, B_0 = 7.5 \times 10^{-8} T , L_0 = 2.5 \times 104\) m, \(\beta p = 0.5\)
  • Integration parameters: \(dt = 0.13 \Omega_{ce}^{-1} (10^{-5} t_0 ), t_{max} = 3 t_0 > 100\) electrons.

4.3 Tasks

Important: Memory limit of your computer.

  • Exercise 1: Compute electron trajectories on the current sheet and plasmoids.
  • Exercise 2: Determine particle energization as a function of time. And locations where it occurs.
  • Exercise 3: Using the guiding center approximation, determine the main contributions to the particle energization (in terms of particle drifts).

You can download the Jupyter notebook here: https://www.app.physik.uni-potsdam.de/~jbenacek/ASPS/lecture04-handson.ipynb

Qin, Hong, Shuangxi Zhang, Jianyuan Xiao, Jian Liu, Yajuan Sun, and William M Tang. 2013. “Why is Boris algorithm so good?” Phys. Plasmas 20 (8): 084503. https://doi.org/10.1063/1.4818428.
Yoshida, Haruo. 1993. “Recent Progress in the Theory and Application of Symplectic Integrators.” Celest. Mech. Dyn. Astron. 56: 27–43. https://doi.org/10.1007/978-94-011-2030-2_3.