Lecture 6: Particle-in-cell – hands-on

Jan Benáček

Institute for Physics and Astronomy, University of Potsdam

November 28, 2024

1 Lecture overview

Table of Contents 1/2

  • 17.10. Introduction + numerical methods summary
  • 24.10. Numerical methods of differential equations — lecture + hands-on
  • 31.10. State holiday
  • 07.11. Test particle approach — lecture
  • 14.11. Test particle approach — lecture + hands-on
  • 21.11. PIC method — lecture
  • 28.11. PIC method — hands-on

Table of Contents 2/2

  • 05.12. Fluid and MHD — lecture (online)
  • 12.12. Fluid and MHD — hands-on ?
  • 19.12. Canceled
  • 09.01. Radiative transfer — lecture + hands-on
  • 16.01. HPC computing — lecture + hands-on
  • 23.01. Advanced — Smooth particle hydrodynamics method — lecture
  • 30.01. Advanced — Hybrid, Gyrokinetics — lecture
  • 06.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture

1.1 Fluid vs Kinetic plasma models

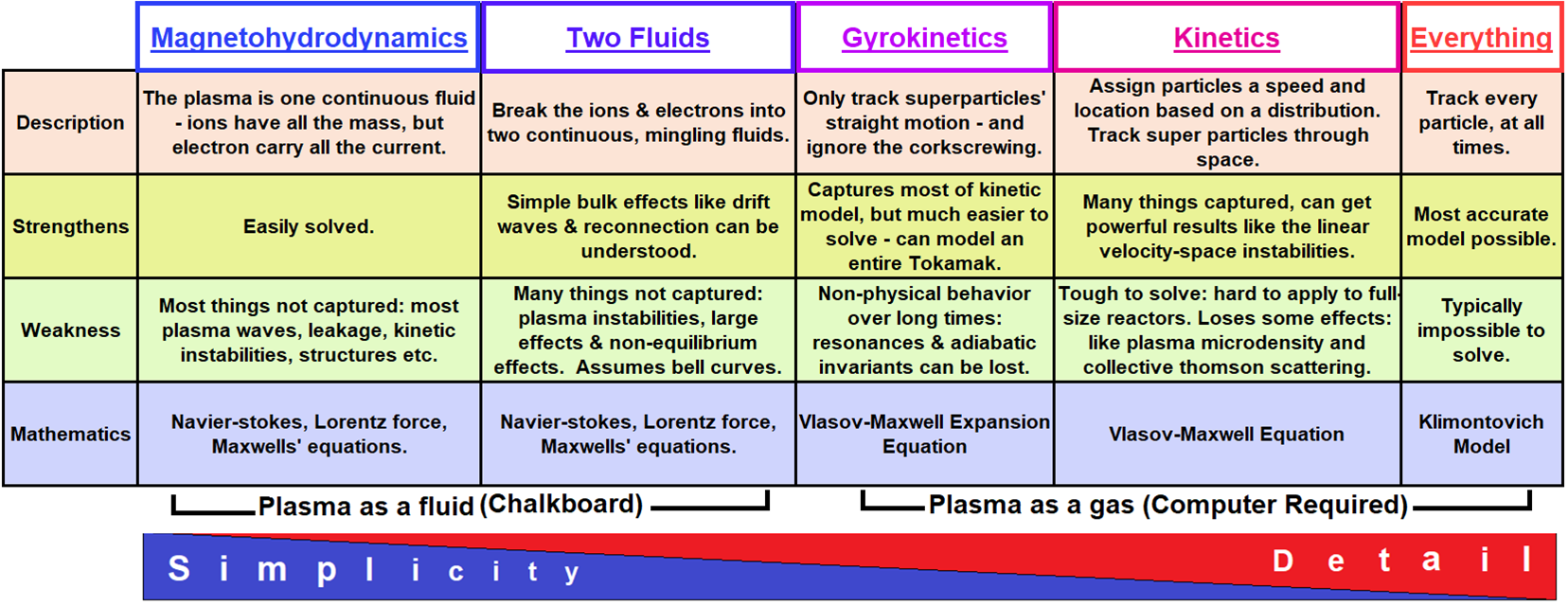
Range of validity of different plasma codes based on typical magnetospheric parameters: \(n=50cm^{-3}\), \(B=50 nT\), \(T_e=T_i=100 eV\) (Winske and Omidi (1996)).

2 Fully-kinetic/Vlasov description - Particle in cell model

2.1 Fully-kinetic/Vlasov description - PIC model

Full equations of motion

\[ \nabla\cdot\vec{E}(\vec{x},t)=\frac{\rho(\vec{x},t)}{\epsilon_0}\\ \nabla\cdot\vec{B}(\vec{x},t)=0\\ \nabla\times\vec{E}(\vec{x},t)=-\frac{\partial \vec{B}(\vec{x},t)}{\partial t}\\ \nabla\times\vec{B}(\vec{x},t)=\mu_0\vec{J}(\vec{x},t)+\mu_0\epsilon_0\frac{\partial \vec{E}(\vec{x},t)}{\partial t} \]

\[ \frac{dv_i}{dt}=\frac{q}{m}\left[\vec{E}(\vec{x}_i,t) + \vec{v}\times\vec{B}(\vec{x}_i,t) \right] \]

\[ \rho(\vec{x},t)=\sum\limits_{\alpha} q_{\alpha}\int\limits dv^3\,\sum_i\delta(\vec{x}-\vec{x_i})\delta(\vec{v}-\vec{v_i})\\ \vec{J}(\vec{x},t)=\sum\limits_{\alpha} q_{\alpha}\int dv^3\,\vec{v}\sum_i\delta(\vec{x}-\vec{x_i})\delta(\vec{v}-\vec{v_i}) \]

2.2 Fluid vs Kinetic plasma models

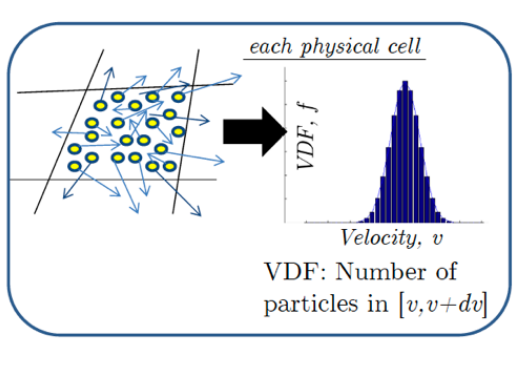
\(Kn\) is the Knudsen number, which indicates how collisional a plasma is. A collisionless plasma has \(K_n\gg1\).

2.3 A typical PIC loop

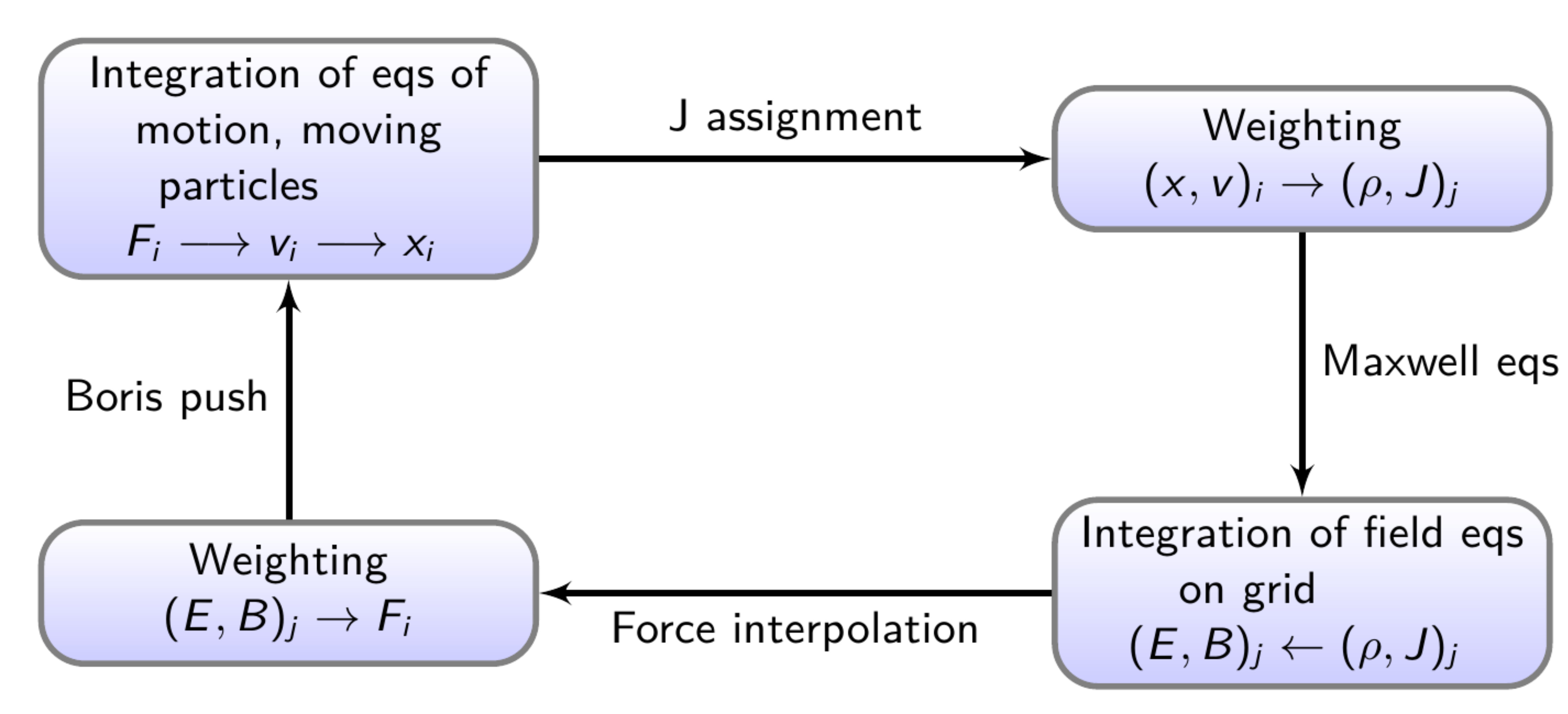
PIC loop.

2.4 Applications

2.5 Beam instabilities

2.6 Idea of micro-instability

  • The linearized 1D electrostatic Vlasov eq is: \[ \frac{\partial f_1}{\partial t} + v\frac{\partial f_1}{\partial x} +\frac{e}{m_e}\frac{\partial \phi_1}{\partial x}\frac{\partial f_0}{\partial v}=0 \]
  • Necessary condition for instability: \[ \left.\frac{\omega}{k}\frac{\partial f_0}{\partial v}\right|_{v=\omega/k}>0 \]

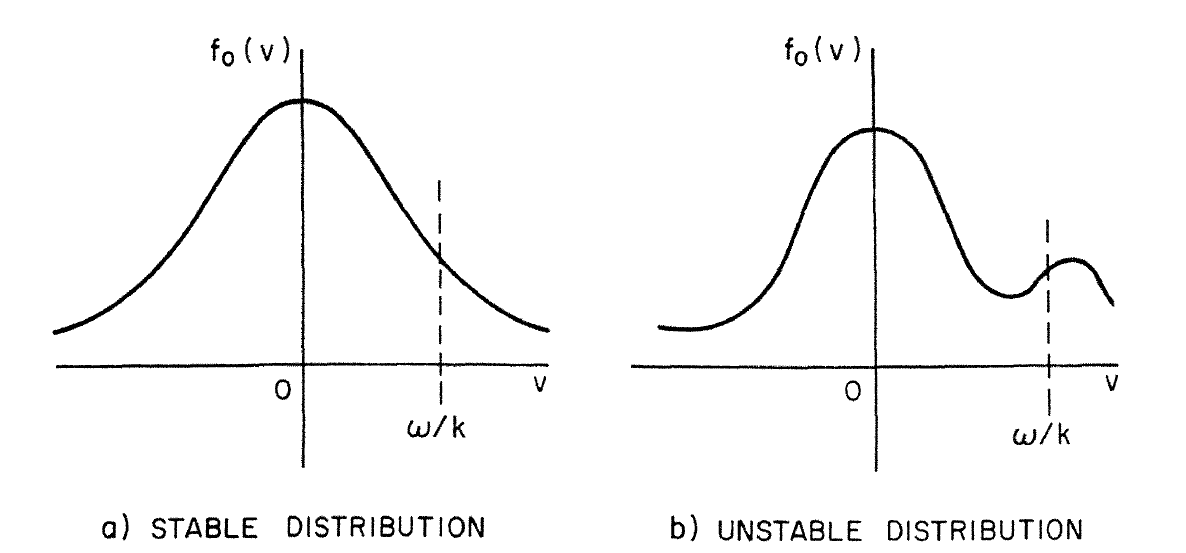
2.7 Two-stream instability

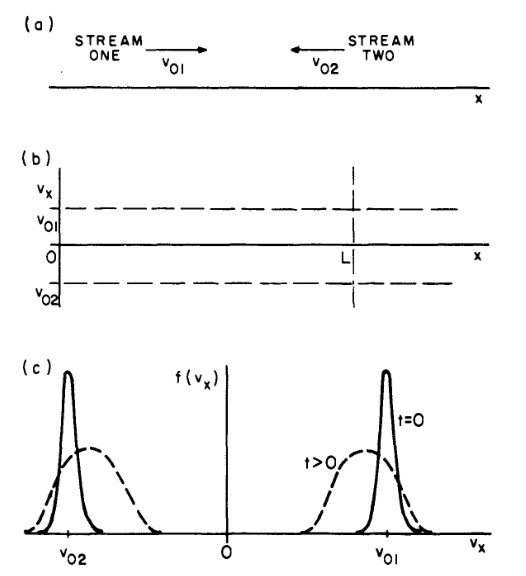
Setup of the two-stream instability (Birdsall and Langdon (1991)).

2.8 Two-stream instability

  • Two counter-propagating streams with similar density Dawson (1962).
  • This system is unstable because any density perturbation in one stream is reinforced by the forces due to the bunching of particles in the other stream, so the perturbation grows exponentially in time \(\Delta n_1\propto n_1\).
  • Dispersion relation (from fluid eqs. or Vlasov with \(\delta\) distributions): \[ \frac{\epsilon}{\epsilon_0} = 1 - \frac{\omega_{p1}^2}{(\omega- \vec{k}\cdot\vec{V}_{01})^2} - \frac{\omega_{p2}^2}{(\omega- \vec{k}\cdot\vec{V}_{02})^2} \]

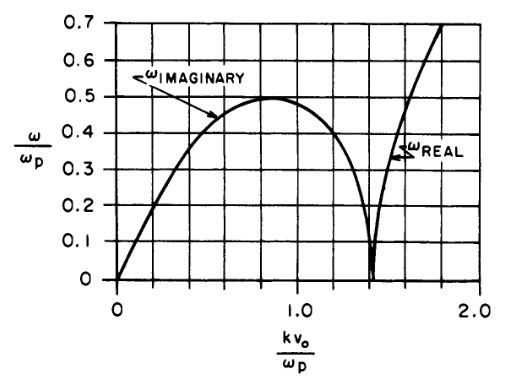
\(\Omega\) and \(\gamma\) of the two-stream instability (Birdsall and Langdon (1991)).

2.9 Two-stream instability simulation

https://www.youtube.com/watch?v=__7GQS15IdE

(https://aip.scitation.org/doi/10.1063/1.3493627)

2.10 Two-stream instability

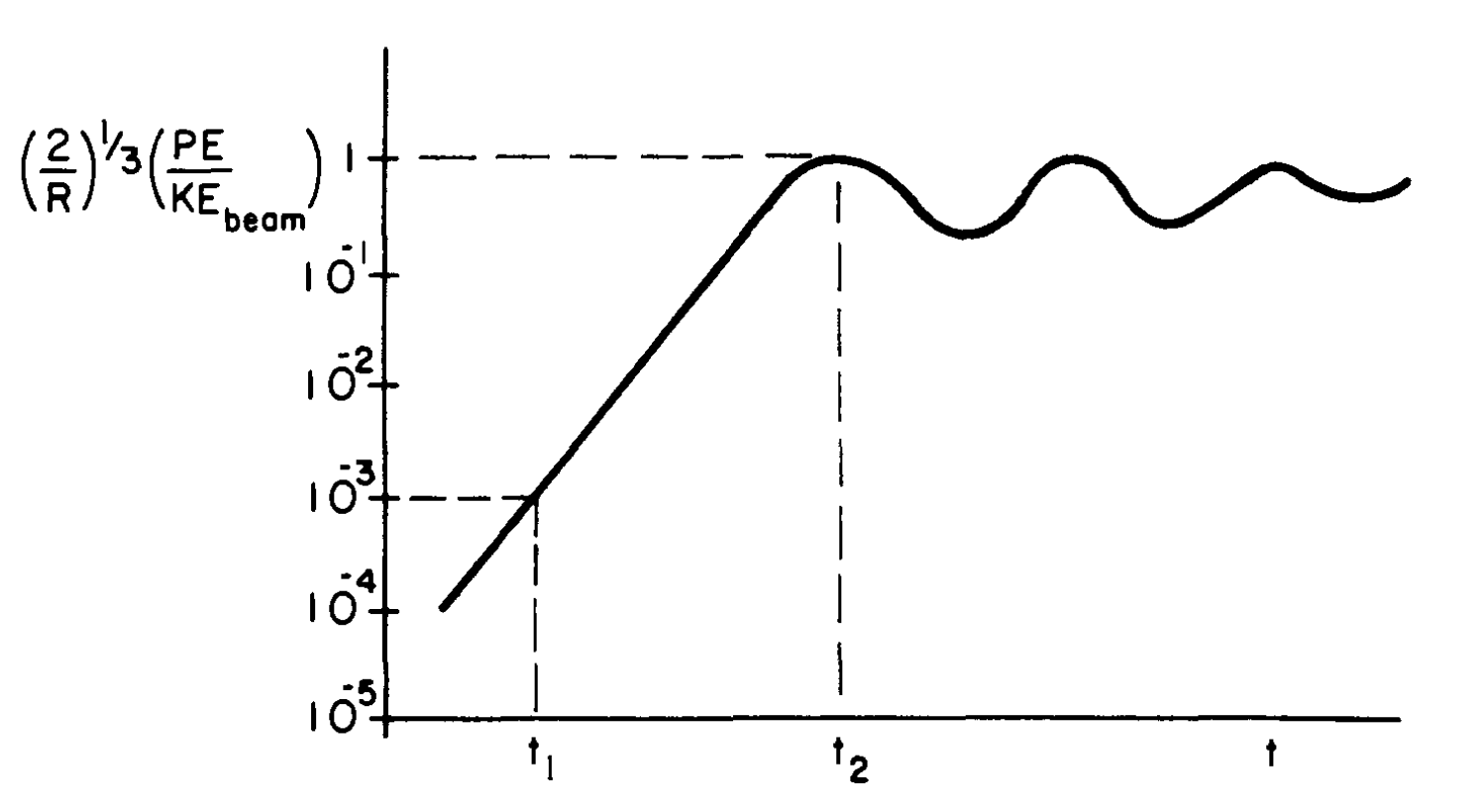
Saturation of the two-stream instability (Birdsall and Langdon (1991)).

2.11 Two-stream instability

  • As the instability grows, the temperature of each beam increases and the drift/mean velocity decreases.
  • The condition for linear growth is \(v_{drift}> 1.3 v_{th}\), but it is observed that growth continues even below this threshold because of non-linear effects (trapping).
  • Growth continues until the streaming is “thermalized”, when the distribution becomes Maxwellian.
  • This thermalization is not due to collisions, but rather due to collective effects: build up of \(\vec{E}\) fields at long wavelengths which scatter particles in the phase space.

2.12 Application: solar radio bursts

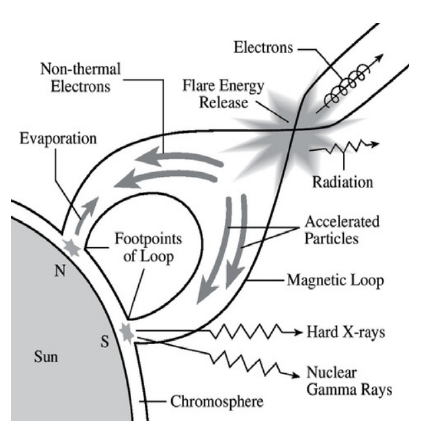
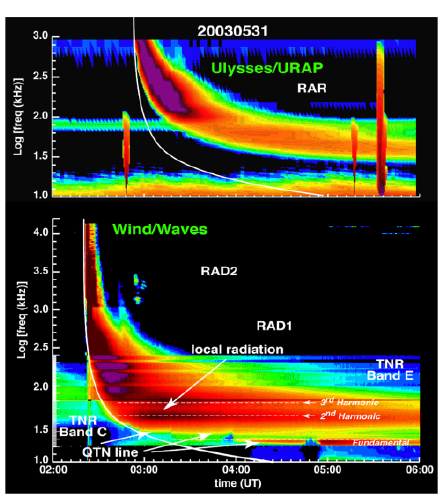
Lang et al. (2010), Reiner and MacDowall (2019)

2.13 Application: pulsar radio emission

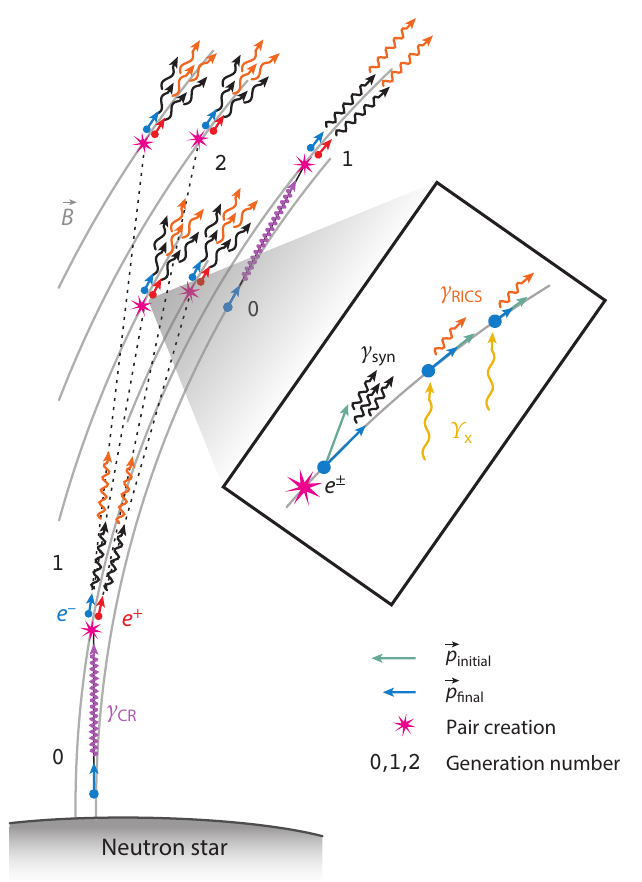
Philippov and Kramer (2022)

NASA, ESO, Timokhin and Harding (2019)

2.14 Application: neutron star magnetospheres

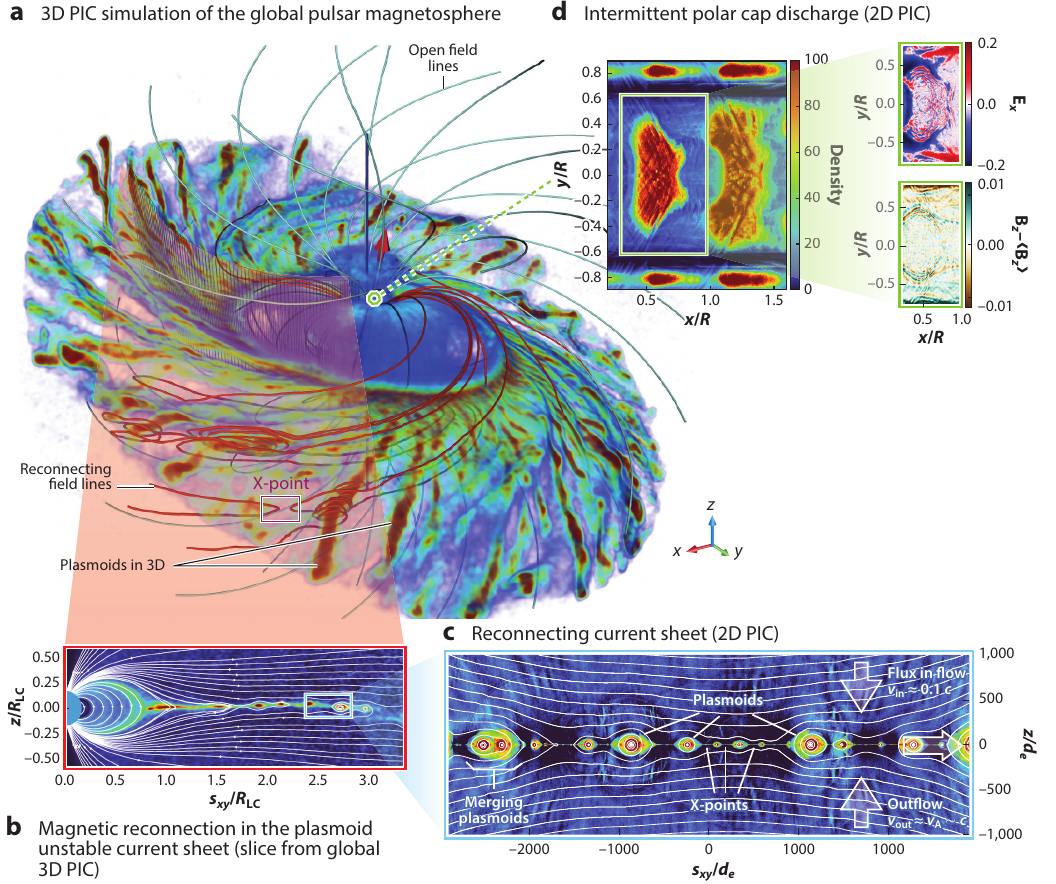
Philippov and Kramer (2022).

2.15 Application: black hole magnetospheres

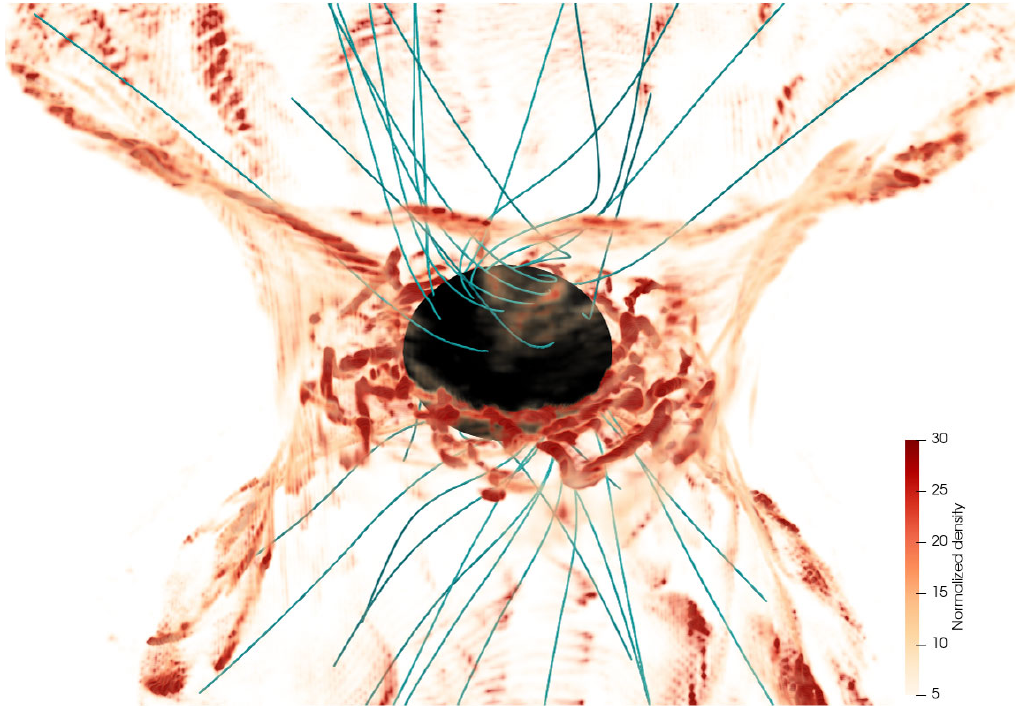
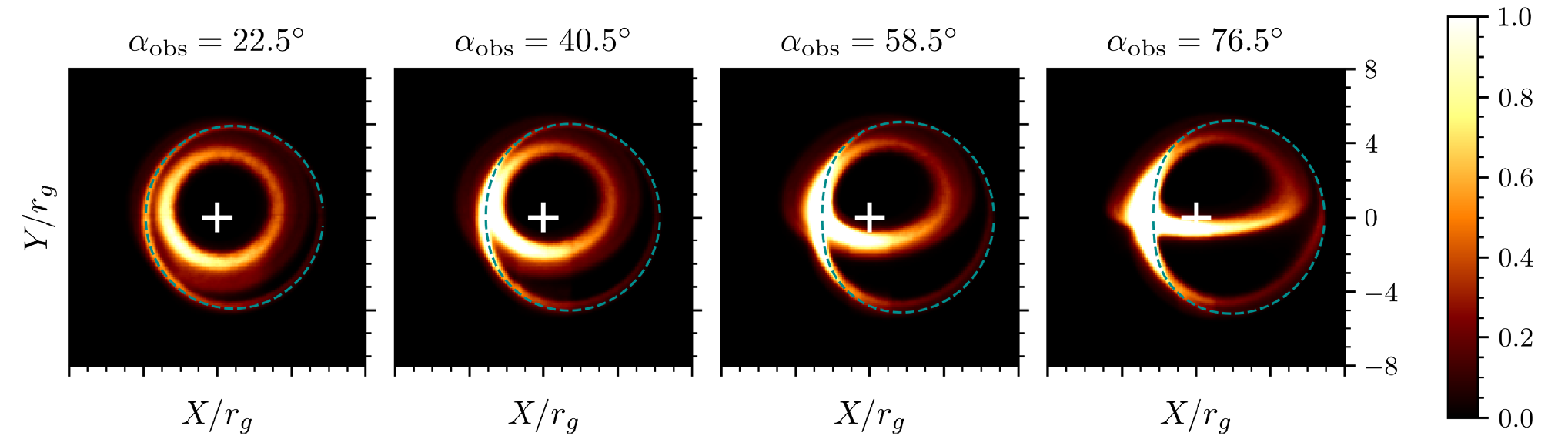
Philippov and Kramer (2022)

Black hole event horizon, magnetic field lines, and plasma density (Crinquand et al. (2022), Philippov and Kramer (2022)).

2.16 Collisionless shocks

2.17 Astrophysical Shocks

ESA: esa.int

2.18 Shock simulation

https://www.youtube.com/watch?v=j1WrS2dyRpw

(Reference paper: Murphy, Dieckmann, and Drury (2010)).

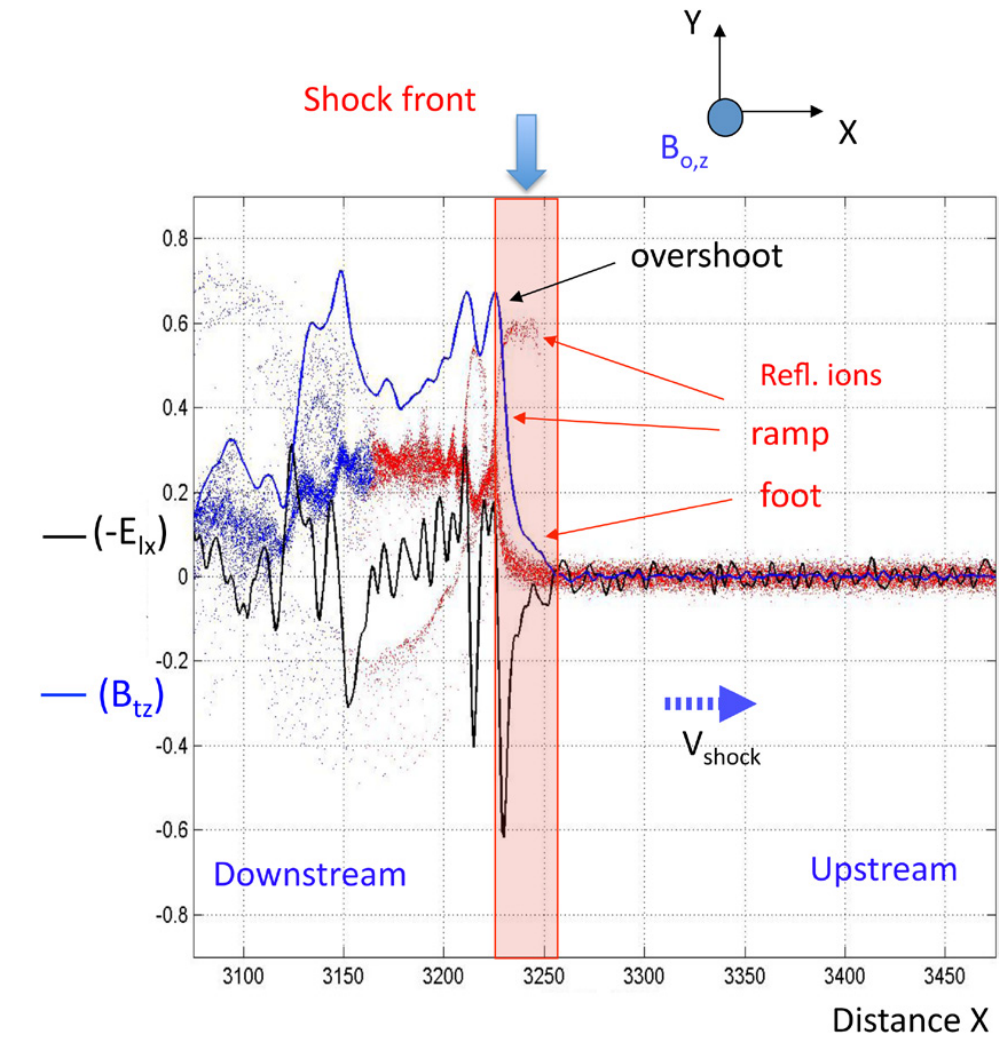
2.19 Shock features

Quasi-perpendicular 1D shock Marcowith et al. (2016).

2.20 Magnetic reconnection

2.21 Magnetic reconnection

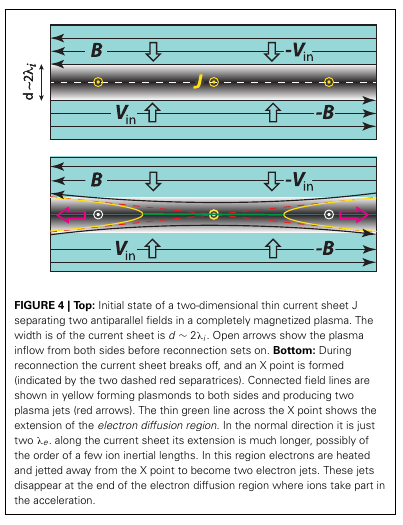
Initial setup (Treumann and Baumjohann (2013)).

2.22 Magnetic Reconnection

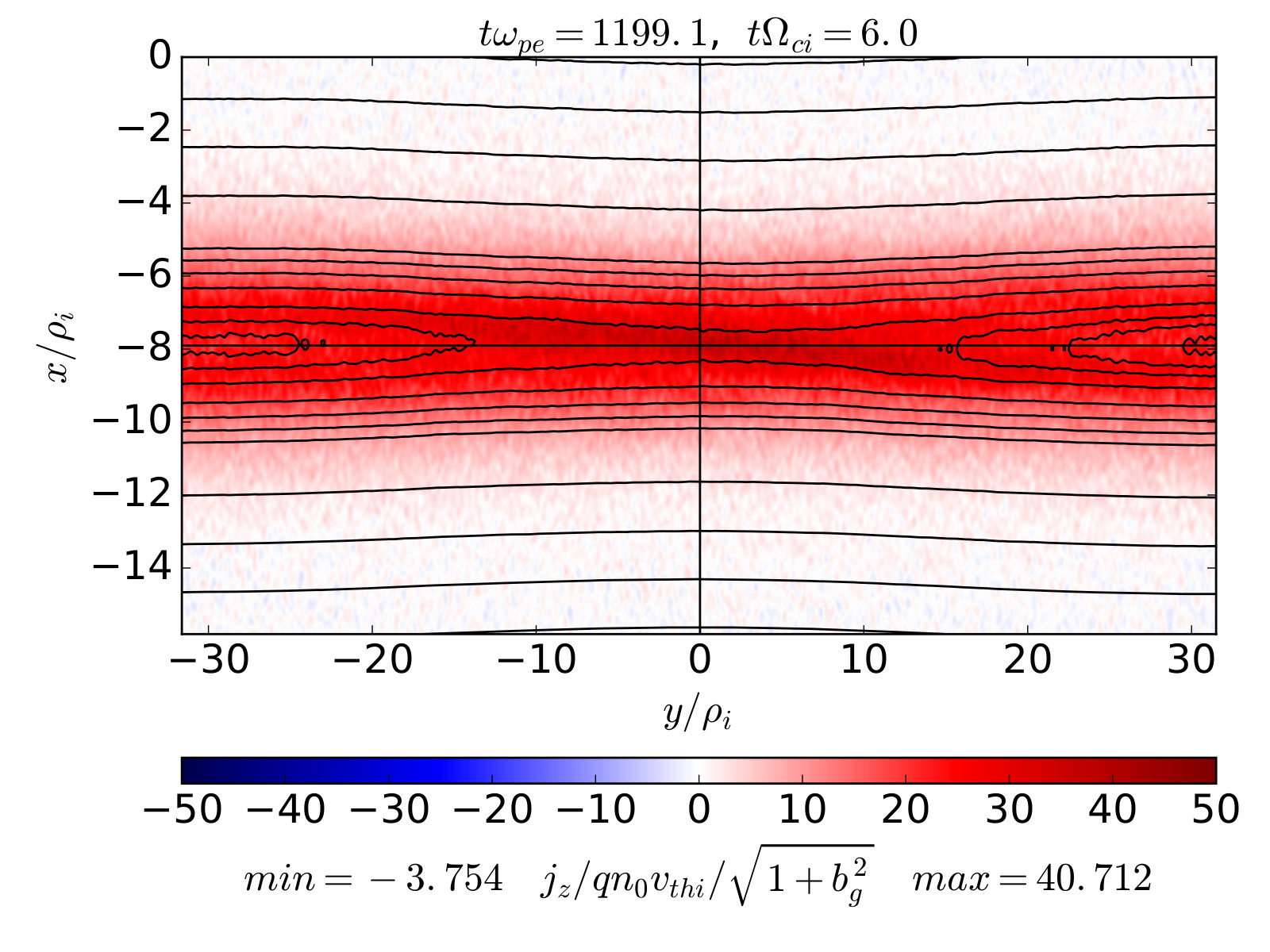
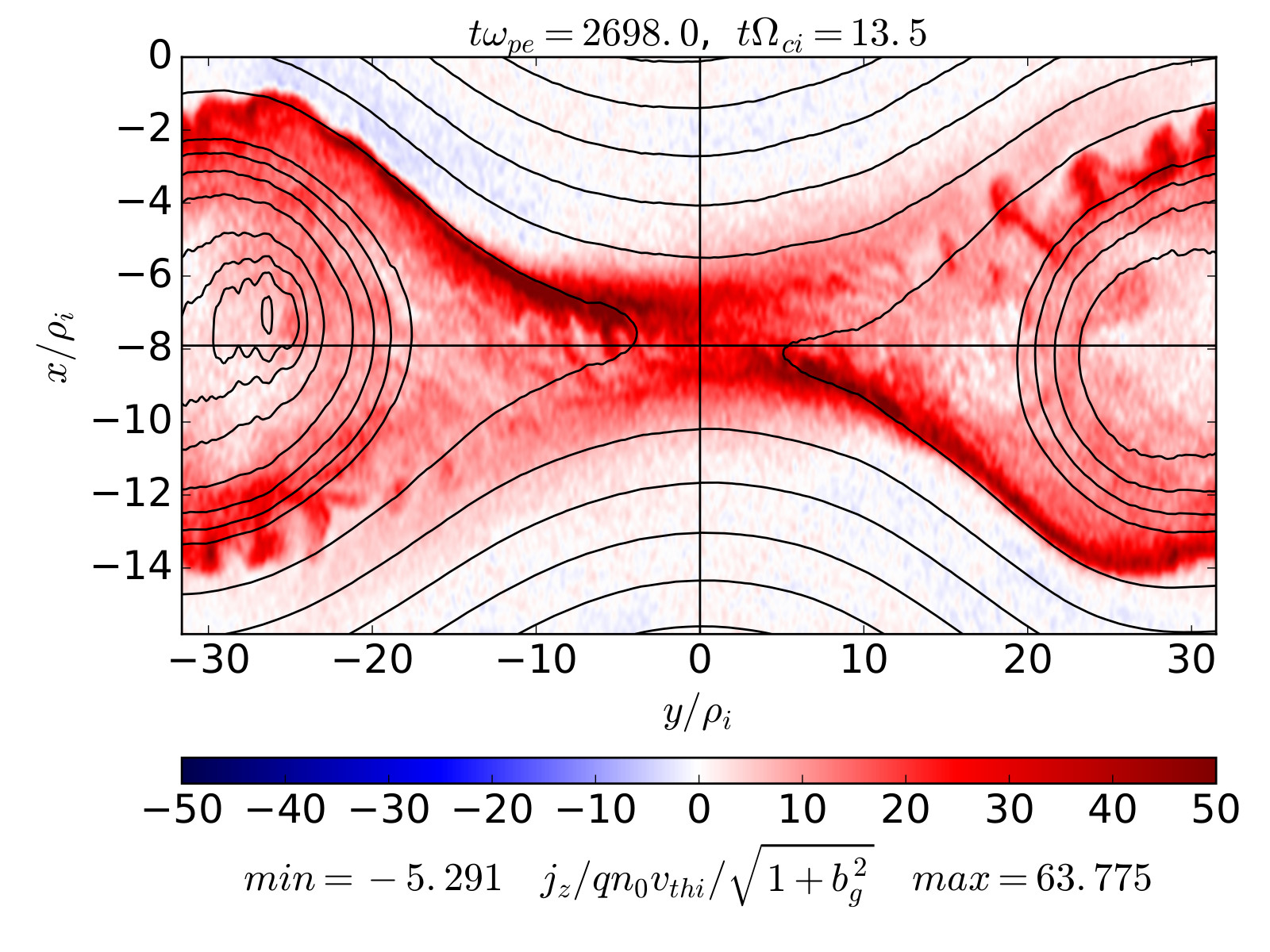
2.23 Magnetic reconnection

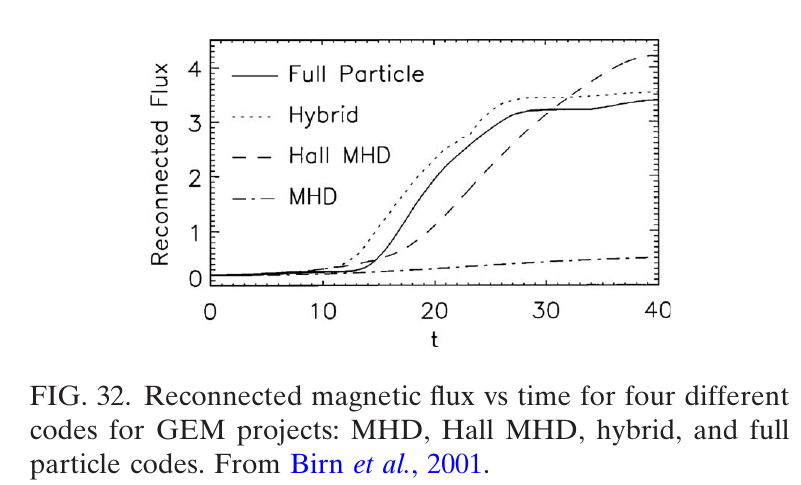
Birn et al. (2001).

2.24 Magnetic reconnection: Earth’s magnetosphere

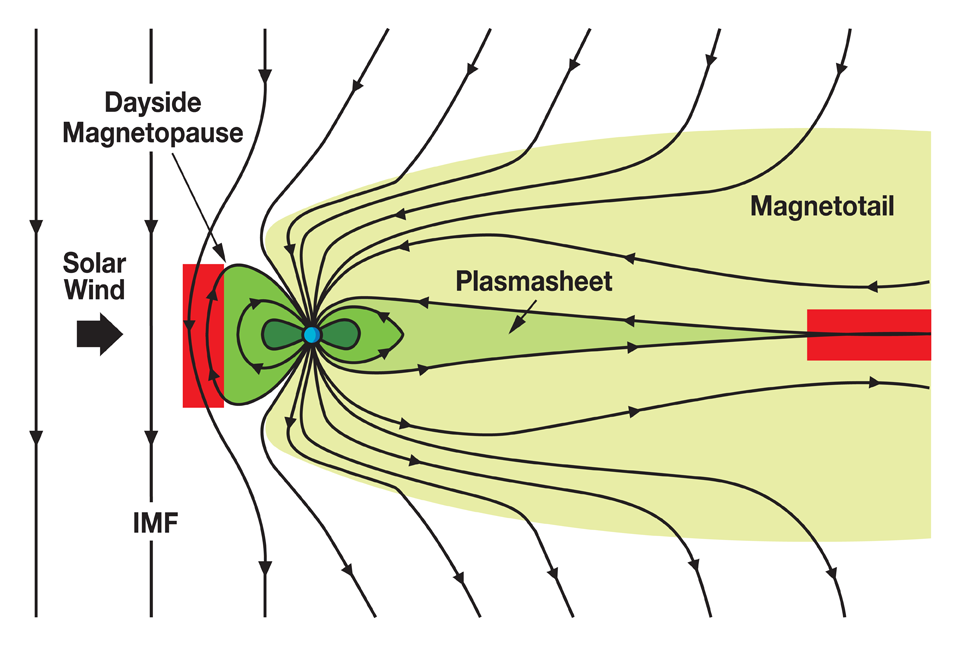
Treumann and Baumjohann (2013).

2.25 Magnetic reconnection: 3D effects

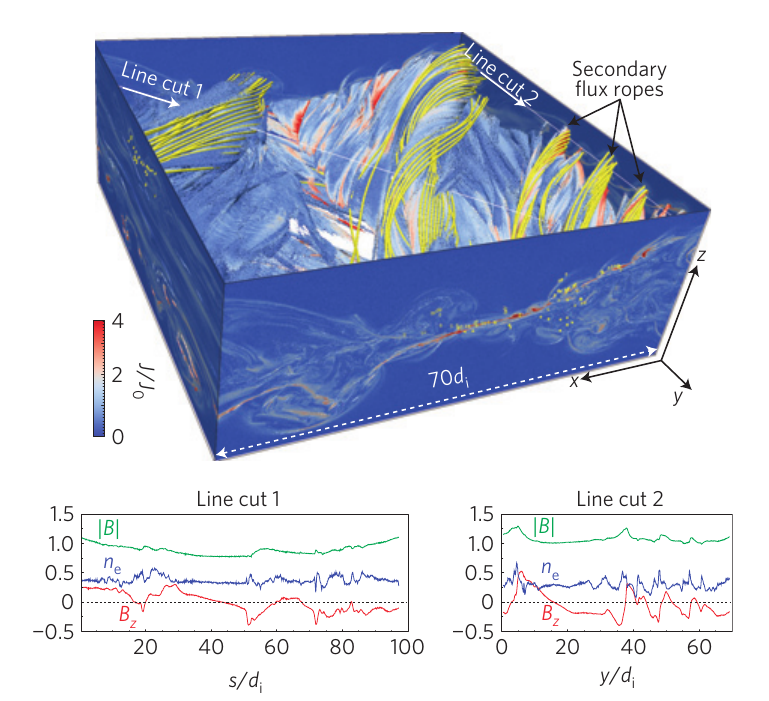
Daughton et al. (2011).

3 Conclusions

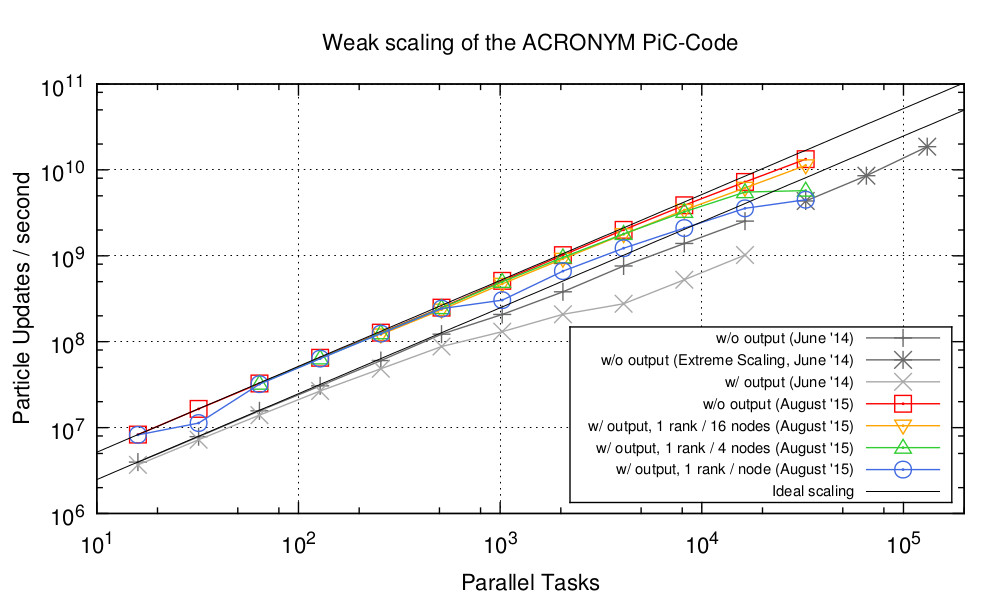
3.1 PIC code ACRONYM

  • Our fully-kinetic PIC code is called ACRONYM: ``Another Code for pushing Relativistic Objects, Now with Yee lattice and Macro particles’’
  • Applications: wave-wave interactions in type II and type III solar radio bursts (radio emission), CME driven shocks in the solar wind, resonant wave-particle interactions, current sheet instabilities and magnetic reconnection, kinetic turbulence, particle acceleration, pulsar radio emission.
  • Published papers with this code in our group: Manthei et al. (2021), Benáček et al. (2021), Benáček, Muñoz, and Büchner (2021), Benáček et al. (2023)

3.2 Other PIC codes

3.3 Bachelor/Master projects:

Investigating magnetospheres of neutron stars:

Polar cat simulation

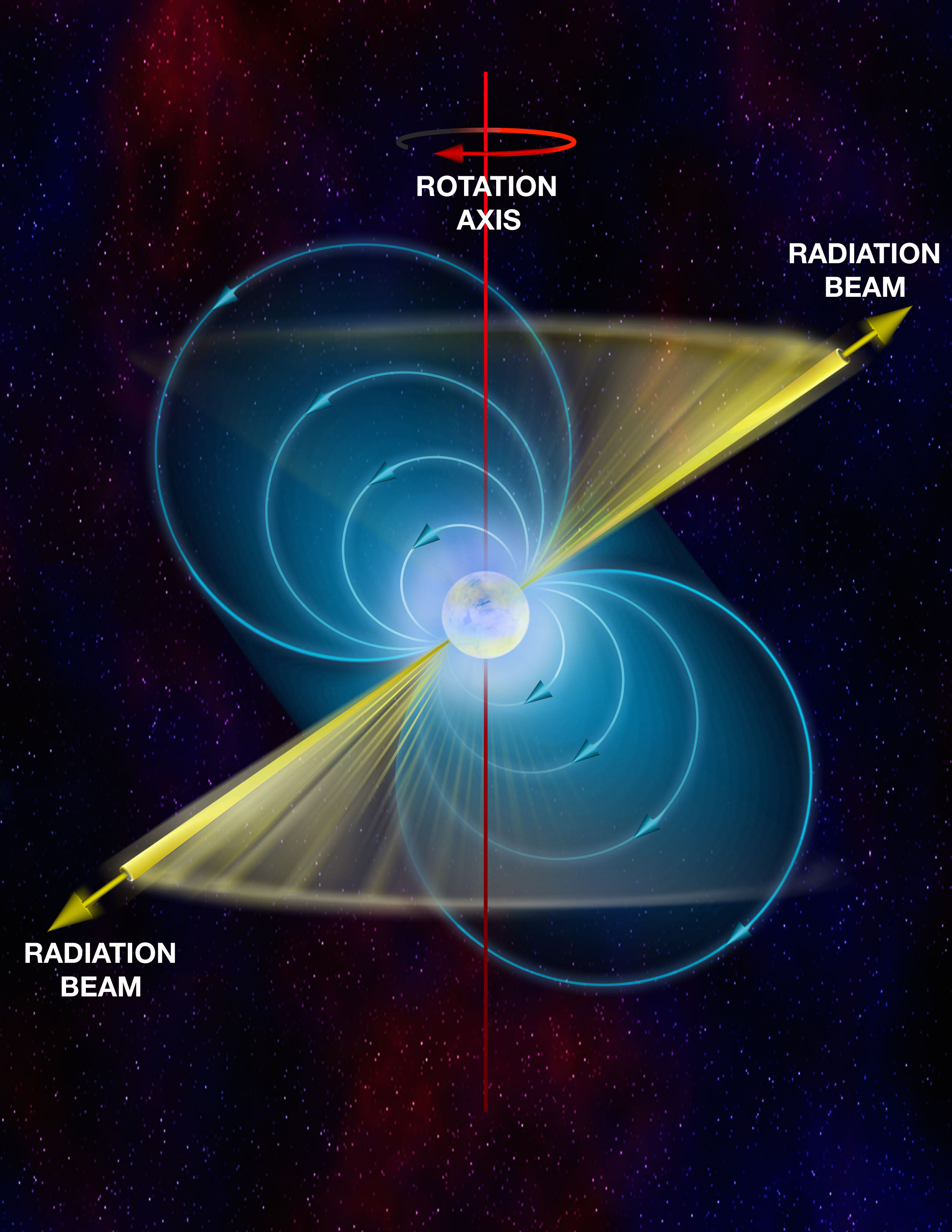
Benáček et al. (2023, in prep.)

3.4 References

Benáček, Jan, Patricio A. Muñoz, and Jörg Büchner. 2021. “Bunch Expansion as a Cause for Pulsar Radio Emissions” 923 (1): 99. https://doi.org/10.3847/1538-4357/ac2c64.
Benáček, Jan, Patricio A. Muñoz, Jörg Büchner, and Axel Jessner. 2023. “Linear acceleration emission of pulsar relativistic streaming instability and interacting plasma bunches” 675 (July): A42. https://doi.org/10.1051/0004-6361/202345987.
Benáček, Jan, Patricio A. Muñoz, Alina C. Manthei, and Jörg Büchner. 2021. “Radio Emission by Soliton Formation in Relativistically Hot Streaming Pulsar Pair Plasmas” 915 (2): 127. https://doi.org/10.3847/1538-4357/ac0338.
Birdsall, C. K., and A. Bruce Langdon. 1991. Plasma Physics via Computer Simulation. Bristol, England: IOP Publishing. https://www.crcpress.com/Plasma-Physics-via-Computer-Simulation/Birdsall-Langdon/p/book/9780750310253.
Birn, Joachim, J. F. Drake, M. A. Shay, B. N. Rogers, R. E. Denton, Michael Hesse, M Kuznetsova, et al. 2001. “Geospace Environmental Modeling (GEM) Magnetic Reconnection Challenge.” J. Geophys. Res. 106 (A3): 3715–19. https://doi.org/10.1029/1999JA900449.
Crinquand, Benjamin, Benoît Cerutti, Guillaume Dubus, Kyle Parfrey, and Alexander Philippov. 2022. “Synthetic Images of Magnetospheric Reconnection-Powered Radiation Around Supermassive Black Holes.” Physical Review Letters 129 (20): 205101. https://doi.org/10.1103/PhysRevLett.129.205101.
Daughton, William, V. Roytershteyn, Homa Karimabadi, L. Yin, B. J. Albright, B. Bergen, and K. J. Bowers. 2011. “Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas.” Nat. Phys. 7 (7): 539–42. https://doi.org/10.1038/nphys1965.
Dawson, John. 1962. “One-Dimensional Plasma Model.” Phys. Fluids 5 (4): 445–59. https://doi.org/10.1063/1.1706638.
Manthei, Alina C., Jan Benáček, Patricio A. Muñoz, and Jörg Büchner. 2021. “Refining pulsar radio emission due to streaming instabilities: Linear theory and PIC simulations in a wide parameter range” 649 (May): A145. https://doi.org/10.1051/0004-6361/202039907.
Marcowith, A., A. Bret, A. Bykov, M. E. Dieckman, L. O’C Drury, B. Lembège, M. Lemoine, et al. 2016. “The microphysics of collisionless shock waves.” Reports on Progress in Physics 79 (4): 046901. https://doi.org/10.1088/0034-4885/79/4/046901.
Murphy, G. C., M. E. Dieckmann, and L. O. C. Drury. 2010. “Magnetic vortex growth in the transition layer of a mildly relativistic plasma shock.” Phys. Plasmas 17 (11): 110701. https://doi.org/10.1063/1.3493627.
Philippov, A., and M. Kramer. 2022. “Pulsar Magnetospheres and Their Radiation” 60 (August): 495–558. https://doi.org/10.1146/annurev-astro-052920-112338.
Reiner, M. J., and R. J. MacDowall. 2019. “New Evidence for Third Harmonic Electromagnetic Radiation in Interplanetary Type III Solar Radio Bursts.” Sol. Phys. 294 (7): 91. https://doi.org/10.1007/s11207-019-1476-9.
Timokhin, A. N., and A. K. Harding. 2019. “On the Maximum Pair Multiplicity of Pulsar Cascades.” The Astrophysical Journal 871 (1): 12. https://doi.org/10.3847/1538-4357/aaf050.
Treumann, Rudolf A., and Wolfgang Baumjohann. 2013. “Collisionless magnetic reconnection in space plasmas.” Front. Phys. 1 (M): 1–34. https://doi.org/10.3389/fphy.2013.00031.
Winske, D., and N. Omidi. 1996. “A nonspecialist’s guide to kinetic simulations of space plasmas.” J. Geophys. Res. 101 (A8): 17287. https://doi.org/10.1029/96JA00982.