Lecture 9: Radiative transfer – Lecture + Hands-on
Institute for Physics and Astronomy, University of Potsdam
January 9, 2025
1 Lecture overview
Table of Contents 1/2
- 17.10. Introduction + numerical methods summary
- 24.10. Numerical methods of differential equations — lecture + hands-on
- 31.10. State holiday
- 07.11. Test particle approach — lecture
- 14.11. Test particle approach — lecture + hands-on
- 21.11. PIC method — lecture
- 28.11. PIC method — hands-on
Table of Contents 2/2
- 05.12. Fluid and MHD — lecture (online)
- 12.12. Fluid and MHD — hands-on given Xin-Yue Shi
- 19.12. Canceled
- 09.01. Radiative transfer — lecture + hands-on
- 16.01. HPC computing — lecture + hands-on
- 23.01. Advanced — Smooth particle hydrodynamics method — lecture
- 30.01. Advanced — Hybrid, Gyrokinetics — lecture
- 06.02. Advanced — Vlasov and Linear Vlasov dispersion solvers — lecture
2 Motivation
2.1 Radiative transfer – motivation

2.2 Solar photosphere
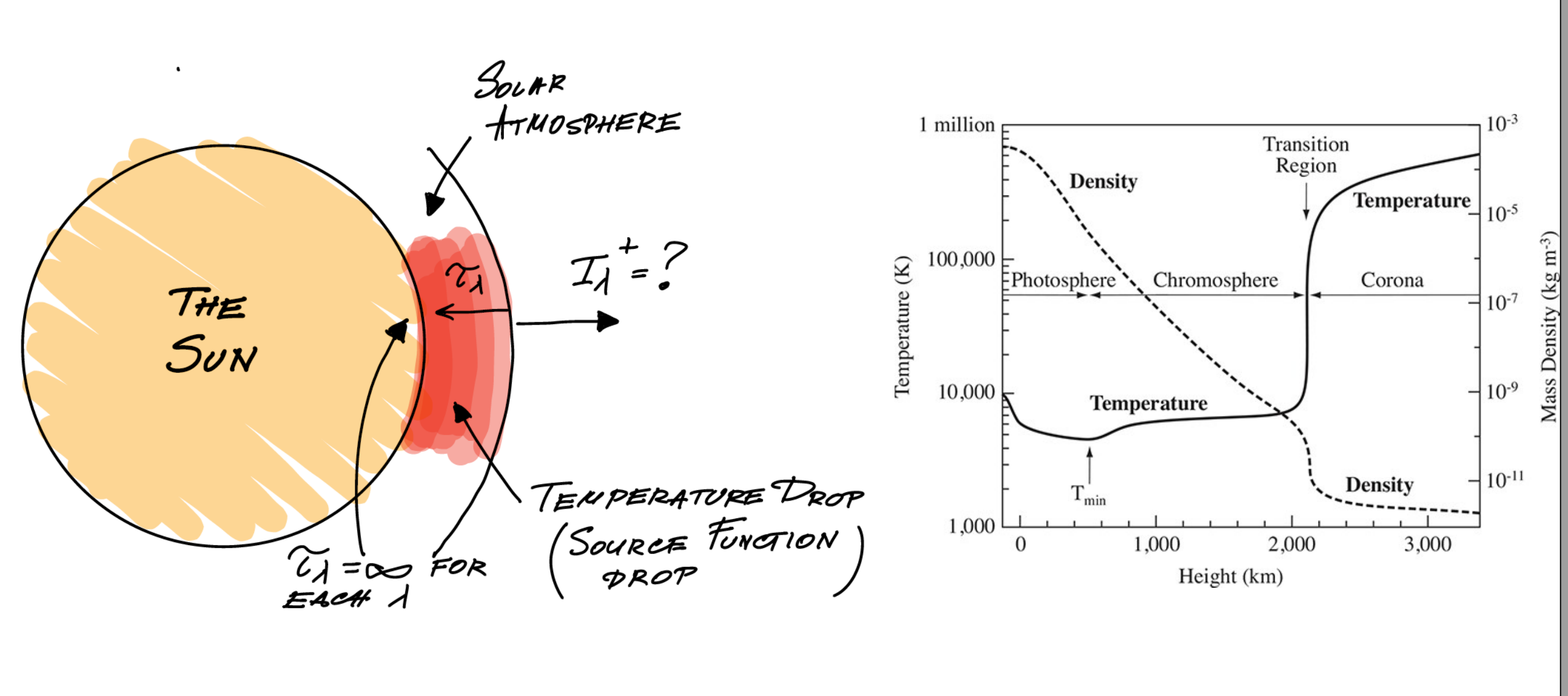
Solar photosphere (nso.edu).
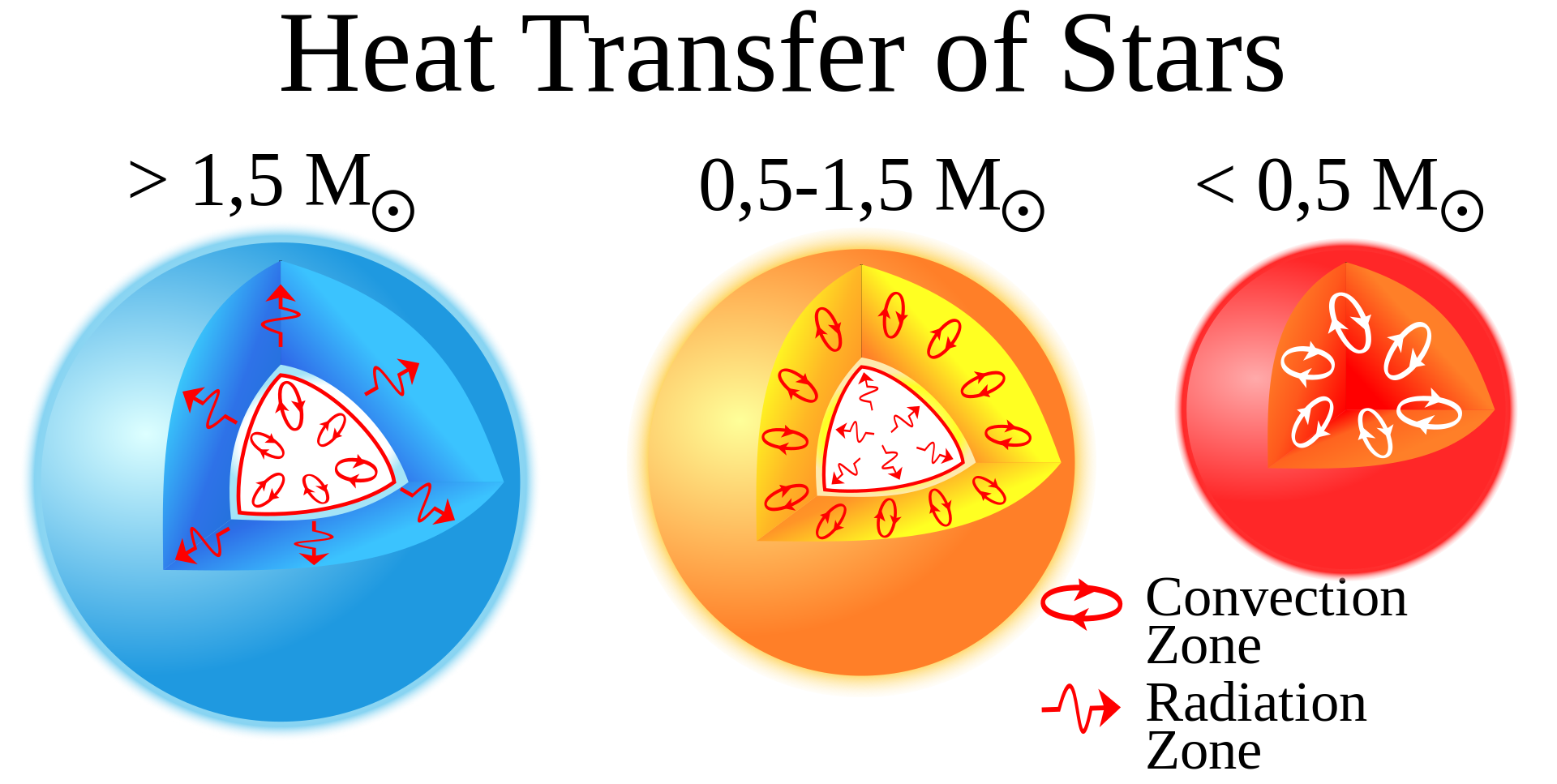
2.3 Stellar radiative transfer
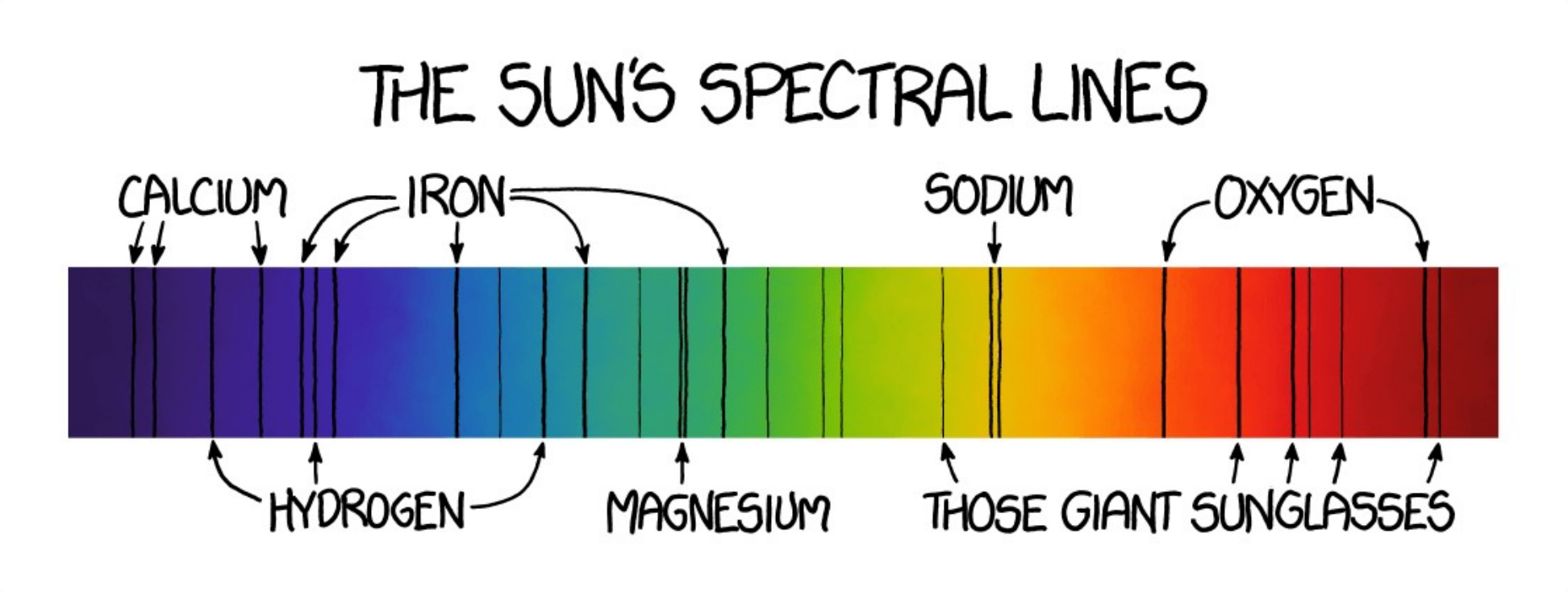
- Stellar spectral types are direct result of the radiative transfer in their photospheres
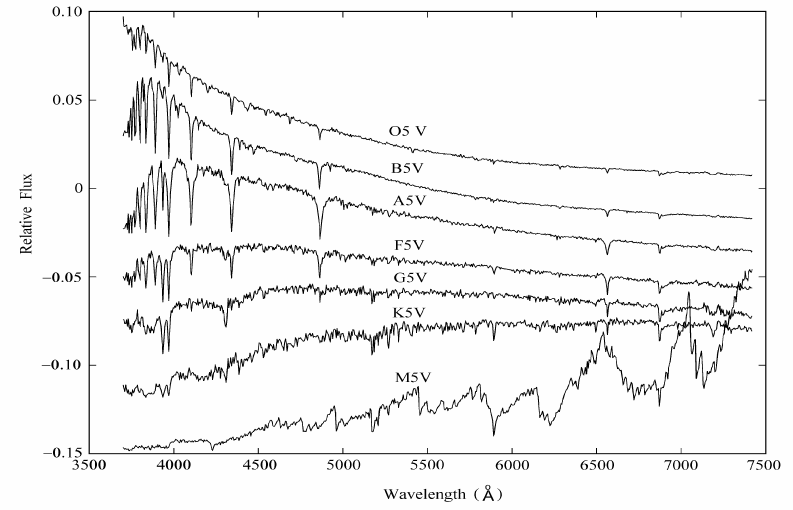
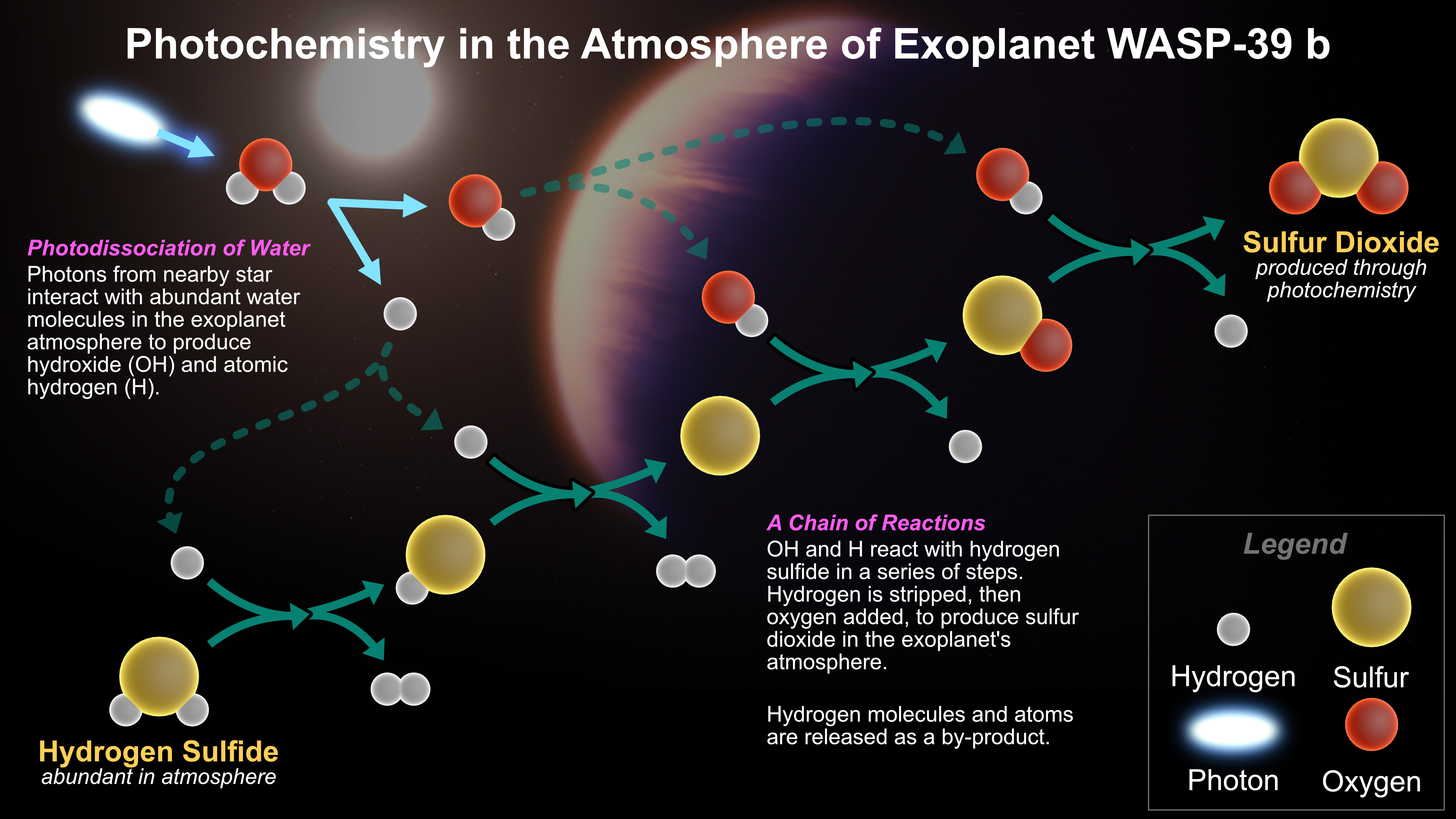
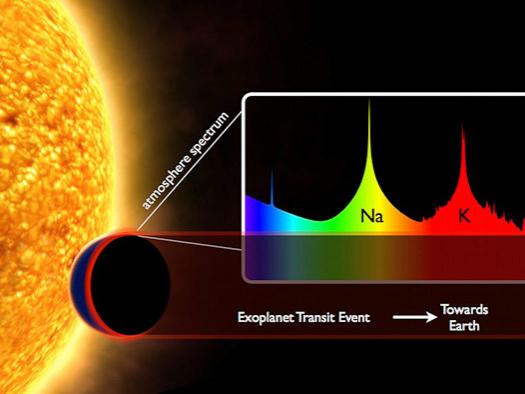
2.4 Exoplanet atmospheres
- Fast development in recent years
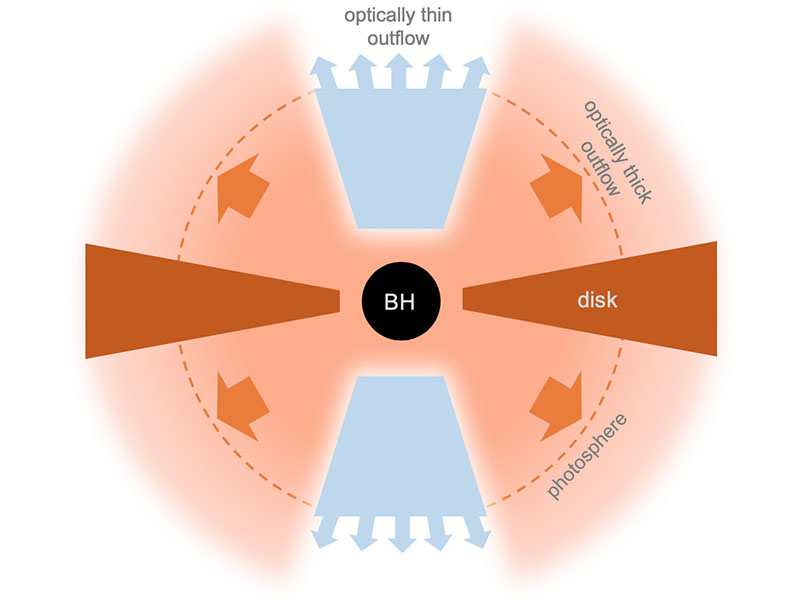
2.5 Accreating compact objects
2.6 Matter in galaxies


2.7 Active galactic nucleus


3 Introduction
3.1 Spectral flux density
Energy passing through a unit surface in unit of time and unit of wavelength/frequency \[ F_\lambda = \frac{dE}{dS \, dt \, d\lambda} \]
- It represents the spatial, temporal, and spectral distribution of the energy flow
- We have to add propagation direction
3.2 Specific monochromatic intensity
Energy passing through a unit surface in unit of time and unit of wavelength/frequency and unit of spatial angle \[ I_\lambda = \frac{dE}{dS \, dt \, d\lambda \, d\Omega} \] with units \[ [ I_\lambda ] = \frac{W}{m^2 \, srad \, nm}. \]
- Generally, it depends on 7 parameters (\(x,y,z,\varphi,\theta,\lambda,t\)).
- Later, we refer it only as ‘intensity’.
3.3 Radiative transfer equation
- It describes how intensity \(I_\lambda\) evolves after
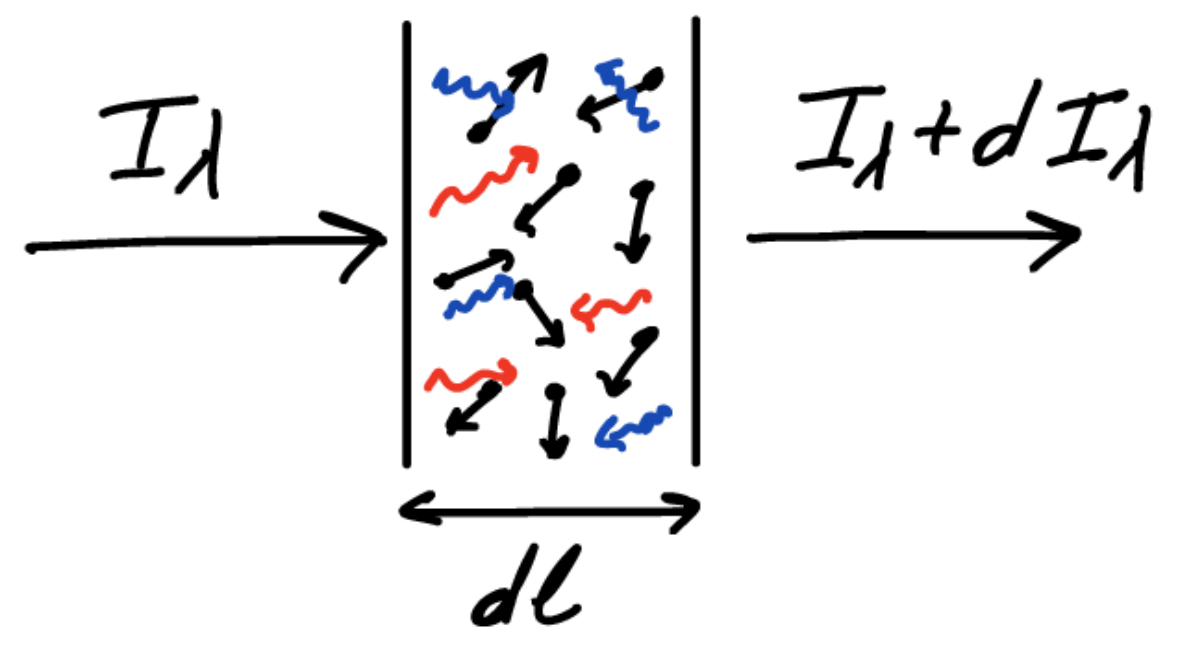
Propagation slab (nso.edu)
\[ \frac{dI_\lambda}{dl} = j_\lambda - \chi_\lambda I_\lambda \]
where:
- \(\lambda\) is the considered wavelength
- \(j_\lambda\) is the emissivity
- \(\chi_\lambda\) is the absorption coefficient / opacity
3.4 Emissivity and absorption
Emissivity can be also expressed as \[ j_\lambda = \frac{dE_{emitted}}{dS \, dl \, dt \, d\Omega \, d\lambda} = \frac{dn_{emitted} \frac{hc}{\lambda} }{dt \, d\Omega \, d\lambda} \]
That leads to a volume emission coefficient \(n_{emitted}\).
The opacity can be expressed as
\[ \chi_\lambda [m^{-1}] = n_{absorbers} [m^{-3}] \times \sigma [m^2] \] where \(\sigma\) is the effective cross-section along the path \(l\).
3.5 Mean free path of a photon
- The higher the opacity is, the shorter distance the photon can travel without interaction.
- Optically thick and thin media.
- The interaction is usually absorption followed by an emission (which can be at a different wavelengths/frequency, emission angle, and intensity).
- More opaque means more photons are trapped.
- For enough photon interactions along the path, the medium gets into an equilibrium state.
- Wavelength dependent
\[ \bar{l_\lambda} = \frac{1}{\chi_\lambda}. \]
3.6 Notes
- Radiative transfer cover all parts of the electromagnetic spectrum.
- Equation of radiative transfer is numerically solved as a set of equations for various wavelengths/frequencies.
- Though, various frequencies can have their specifics.
- Whole zoo of absorption and emission mechanisms.
4 Solving radiative transfer equation
4.1 Different form of the radiative transfer equation
- Often, a different form of the equation is used for solving.
- Let’s divide the radiative transfer equation by \(\chi_\lambda\), we obtain \[ \frac{dI_\lambda}{\chi_\lambda dl} = \frac{j_\lambda}{\chi_\lambda} - I_\lambda \]
- That leads to equation \[ \frac{dI_\lambda}{d\tau_\lambda} = S_\lambda - I_\lambda \] where \(\tau_\lambda\) is the optical depth and \(S_\lambda\) is the source function (same unit as the intensity).
- By using this equation, we solve the transfer with respect to \(\tau_\lambda\) instead of \(l\).
- That allows to cover regions where \(\tau_\lambda\) significantly change without dealing with real spatial scales.
- For example, in stellar atmosphere, the lower atmospheric layers have large optical depth while they are small in thickness. In contrast, in stellar wind, the optical depth is mostly small, but the spatial size is huge.
- \(\Rightarrow\) From optical depth is not easy to get spatial scales.
4.2 Simple analytical solutions
\[ \frac{dI_\lambda}{dl} = j_\lambda - \chi_\lambda I_\lambda \]
For \(\chi_\lambda = 0\) and \(j_\lambda =\) const, the transfer equation is \[ \frac{dI_\lambda}{dl} = j_\lambda \] Which has a solution \(I = j_\lambda L\), where \(L\) is the propagation distance.
For \(j_\lambda = 0\) and \(\chi_\lambda =\) const, the transfer equation is \[ \frac{dI_\lambda}{dl} = \chi_\lambda I_\lambda \] Which has a solution \(I = I_0 e^{-\chi_\lambda L}\), where \(I_0\) is the initial intensity.
4.3 A formal solution
More general form.
Assume a radiative transfer from \(\tau_\lambda = 0\) to \(\tau_\lambda = L\) \[ I_\lambda = I_0 e^{-\tau_\lambda} + \int_0^{\tau_\lambda} S(t) e^{-l} dl. \]
To solve the equation, we need
- Initial/input intensity as a boundary condition.
- Knowledge of the source function \(S\) as a function of the optical depth — this can be extremely complex function, e.g., absorption at some wavelengths can be emission at another.
- What can we conclude from the solution?
4.4 A formal solution
\[ I_\lambda = I_0 e^{-\tau_\lambda} + \int_0^{\tau_\lambda} S_\lambda(t) e^{-l} dl. \]
- More optically thick object — less dependent on the boundary condition because \(I_0 e^{-\tau_\lambda}\).
- The source function at the same boundary \(S(\tau=0)\) matters much more, but still very little.
- The result does not depend on the boundary for \(\tau \gg 1\); in practise for \(\tau >\) a few.
- Everything is strongly wavelength dependent.
- The source term \(S_\lambda(\tau)\) depend also on all other wavelength \(\lambda\).
- \(\Rightarrow\) the equation must be solved implicity — typically interating from an initial guess to final solution.
4.5 Opacity and emissivity
- Where do the opacity and emissivity (coefficients of absorption and emission) come from?
- One of the most basic sources are due to the spectral lines
4.6 Practical implications for solving
- We have spatial distribution of plasma quantities — temperature, pressure, velocity, magnetic field,…
- They can obtained, e.g., from the plasma simulation.
- We can obtain the source function from those quantities (e.g., the black-body radiation).
- We can integrate the radiative transfer equation to get emitted part of the radiation.
4.7 Spectral lines
- At specific frequencies.
- Spontaneous emission - isotropic, does not depend on the radiation background
- Stimulated emission - follows the distribution of incoming radiation, depends on the radiation background
- The radiation source is the atom transition from higher-energy state to lower-energy state.
\[ j_\lambda = \frac{d^3 n_{emitted}}{dt} \frac{\frac{hc}{\lambda} }{d\Omega \, d\lambda} \] where \(n_{emitted}\) is number of emitting/radiation atoms/sources.
4.8 Emission coenficient
- For isotropic spontaneous emission (\(d\Omega = 40\pi\)): \[ \frac{dn_{emission}}{dt} = n A_{ul} \] where \(A_{ul}\) is the emission rate — Einstein coefficient of spontaneous emission.
- Profile of the spectral line \[ \frac{d n}{d \lambda} = \phi_\lambda, \qquad \int_{-\infty}^{\infty} \phi_\lambda d\lambda = 1. \]
- Combining all together we get \[ j_\lambda = \frac{hc}{4\pi \lambda} n_u A_{ul} \phi_{ul,\lambda}. \]
4.9 Absorption coefficient
- Similar analogy to the emission, assuming that we have an absorption coefficient \[ \chi_\lambda = \frac{hc}{4\pi \lambda} n_u B_{ul} \phi_{ul,\lambda}. \]
4.10 LTE vs NLTE approaches
- (N)LTE — (non-) local thermodynamic equilibrium.
- Influences how are energy excitation/ionization states filled.
LTE
- Enough collisions to achieve the equilibrium (dense plasma).
- Boltzmann excitation equation.
- Saha ionization equation.
NLTE
- Not so strongly collisional media.
- Necessary to calculate the occupancy of atom/source energy states.
- Does not follow the Boltzmann and Saha equations.
4.11 Combination with various plasma simulations
- Typically, for plasma conditions/region, we calculate the radiative transfer.
- Many state-of-the-art simulations also include radiative feedback on the plasma.
- Relation to various simulation types:
- Kinetic simulations — radio, X-ray, \(\gamma\)-ray,
- Fluid/MHD simulations — infrared, visual, ultraviolet,
- Testing particles — X-ray and \(\gamma\)-ray.
- General-relativistic simulations — radiative transfer in curved space–time.
5 Hands-on session
5.1 Hands-on session
- We will use Jupyter notebooks by Ivan Milic
- Get the Jupyter notebook
$ mkdir lecture09
$ cd lecture09
$ git clone https://github.com/ivanzmilic/collage
$ cd collage
$ jupyter lab- We will use ‘Hands_on_1_spectrum_synthesis.ipynb’
- As homework, you can go through other notebooks